
Banca di problemi del RMT
gp49-it
 |
Banca di problemi del RMTgp49-it |
|
Envoyer une remarque ou une suggestion
Trovare quante distanze differenti ci possano essere tra due centri dei 25 quadrati di una griglia quadrata, di 5 x 5.

- Capire che le “distanze” menzionate nell’enunciato si misurano tra due alberi in “linea retta” e che si tratterà di confrontare le lunghezze dei segmenti determinati da due punti sul disegno.
- Rendersi conto che c’è un gran numero di distanze (segmenti) tra due qualunque dei 25 punti e che molte di queste distanze saranno uguali (segmenti della stessa lunghezza). La più corta è di 1 (con unità il lato di un quadretto della griglia), la maggiore è quella tra due centri di quadrati “opposti” seguendo una diagonale della griglia.
- Capire che per evitare di contare diverse volte una medesima distanza, ci si può limitare alle distanze tra un punto al centro di un quadrato “in un angolo” (per esempio quello in alto a sinistra) e gli altri 24 punti. Poi, in virtù della simmetria rispetto a una diagonale, si può ancora limitare i confronti interessandosi solo a 15 punti: i punti scelti in un angolo e altri 14, sopra e/o sotto la diagonale.
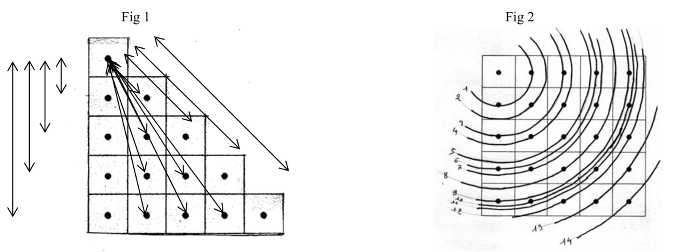
- Verificare che dal punto scelto agli altri quattro della sua colonna ci sono 4 distanze “verticali” differenti (1, 2, 3, 4) poi che dal punto scelto agli altri quattro della colonna vicina ci sono ancora 4 distanze differenti, poi 3 distanze differenti con i 3 punti al di sotto della diagonale della terza colonna, poi 2 con i punti della quarta colonna e 1 con il punto opposto (in diagonale), cosa che porta a 14 distanze differenti (Fig 1).
- I confronti possono essere fatti via via visualmente. L’uso del righello è necessario solo per le due distanze tra il punto fissato e, rispettivamente, quello in basso della colonna vicina e il penultimo seguendo la diagonale (√17 et √18). - Un altro modo di determinare il numero di distanze è usare il compasso (Fig 2).
Su 276 classi di 5 sezioni
| Categoria | 0 | 1 | 2 | 3 | 4 | Nb.classi | Media |
|---|---|---|---|---|---|---|---|
| Cat 7 | 71 (44%) | 22 (14%) | 38 (24%) | 8 (5%) | 21 (13%) | 160 | 1.29 |
| Cat 8 | 38 (33%) | 19 (16%) | 33 (28%) | 11 (9%) | 15 (13%) | 116 | 1.53 |
| Totale | 109 (39%) | 41 (15%) | 71 (26%) | 19 (7%) | 36 (13%) | 276 | 1.39 |
| Si ricorda che il problema è stato affrontato nelle condizioni particolari del RMT: intera classe, allievi in completa autonomia, da 5 a 7 problemi da risolvere, un solo foglio risposta per problema. | |||||||
Questo problema è stato analizzato nell'ambito di un progetto di ricerca del "Gruppo di Geometria Piana per Grandi" sul concetto di distanza (vedi articolo in bibliografia, pagine da 93 a 102) e proposto specificamente in due classi di categoria 7 della Franche Comté (f.f)
Un ostacolo risiede nell'appropriazione dell'espressione "Quante distanze diverse ci sono tra due alberi?", poiché gli allievi spesso pensano a due alberi che si susseguono, verticalmente o orizzontalmente.
Questo ostacolo impedisce quindi agli agglievi di entrare nel processo di ricerca delle "distanze". Una volta superato, è comunque necessario distinguere tra distanze "diverse" e trovare una procedura che eviti di contare le stesse distanze più volte.
Malgrado le medie basse riscontrate nell’ambito della prova del RMT, la situazione proposta dell’enunciato può essere costruttivamente utilizzata in classe.
Dopo qualche minuto di ricerca individuale o in gruppo, una messa in comune permetterà a tutti di appropriarsi del compito: percepire le “distanze”/”lunghezze di segmenti” ed eliminare i segmenti congruenti partendo da un punto fisso. Se si considerano i segmenti come diagonali di rettangoli, il confronto delle lunghezze di due segmenti “vicini” (o diagonali di due rettangoli aventi la medesima larghezza) si può fare per deduzione.
Il solo confronto che richiede un’attenzione particolare è quello delle due diagonali di un rettangolo (1;4) e del quadrato (3;3). La differenza è visibile con l’uso del compasso o con la costruzione precisa di un ingrandimento della griglia quadrata. Il confronto può anche essere fatto per costruzione, su una quadrettatura di quadrati costruiti su ciascuna diagonale, poi con conteggio dei quadrati interi e di parti di quadrati raggruppati. Le aree di questi quadrati sono rispettivamente 17 e 18 (in quadrati della quadrettatura) e si può concludere, per deduzione, che i due segmenti sono differenti (anche senza il teorema di Pitagora, né calcoli di radici quadrate!).
Nella famiglia CA Confronto di aree, si trovano numerosi problemi di determinazione di aree di figure su una quadrettatura, per scomposizione in figure semplici le cui aree si addizionano o si sottraggono a partire da quella di un rettangolo “circoscritto”. Si veda ad esempio il problema Confronto di figure .
Esempi di attività per un percorso didattico con la classe
Da sperimentare in classe, secondo le modalità stabilite dall'insegnante; con invio descrizione e commenti per mostrare la rilevanza dell'attività ai fini dell'acquisizione di saperi (indicati in corsivo).
(Non possiamo - o addirittura non dobbiamo - fermarci alla questione del "problema della gara"! Il conteggio ha dato come risposta 14, che l'intera classe può accettare dopo una prima messa in comune dei risultati. Tuttavia, la discussione non garantisce che il concetto di "distanza" in geometria sia stato "costruito" o "ricostruito" o ancora "arricchito" da parte degli allievi. Per la maggior parte di essi, infatti, la distanza rimane allo stato di "distanza, visiva o dinamica" relativa ai loro movimenti, ai loro giochi, alla distanza di persone o oggetti. L'oggetto delle seguenti proposte è innanzitutto la distanza.)
a) Riprendere il problema, ma con una quadrettatura 6 x 6 (almeno) invece di una 5 x 5. Con una quadrettatura 6 x 6, si arriva a 20 distanze, di cui solo 19 differenti, ed è qui che nasce la necessità di andare oltre il confronto visivo per arrivare a una "misura" dei segmenti corrispondenti.
I saperi: passare dal conteggio delle diverse distanze tra due chiodi al loro confronto, quindi alla loro misura, determinare le relazioni tra la misura di un lato di un quadrato e quella della sua superficie (area), scoprire i numeri non interi, non decimali e non razionali, trovare approssimazioni di numeri che la calcolatrice non può visualizzare con precisione.
b) Disegnare alcuni quadrati i cui lati siano distanze dalla lista. Ad esempio, nella figura seguente:
- il quadrato costruito sul segmento (1; 0) o (0; 1) della seconda riga, in alto a sinistra,
- il quadrato costruito sul segmento (1; 1) della terza riga, in alto al centro,
- il quadrato costruito sul segmento (2; 1) o (1; 2) della quinta riga, in basso a sinistra.
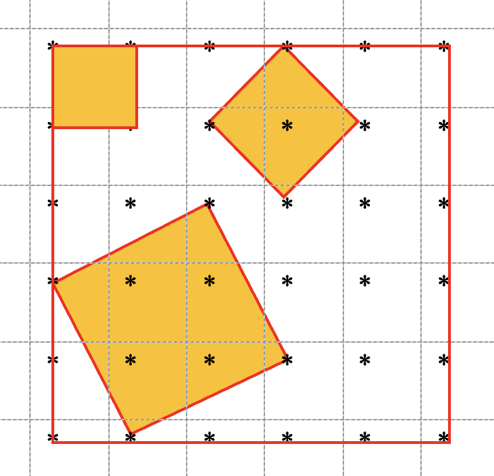
I saperi: costruzione di segmenti perpendicolari e isometrici tra due punti di una quadrettatura e percezione delle relazioni tra le loro "coordinate", determinazione dell'area di quadrati con lati "obliqui" a partire da quadrati "circoscritti" più grandi con lati "orizzontali" e "verticali", ritagliando quattro triangoli isometrici (scomposizione e ricomposizione di figure bidimensionali).
c) Redigere un inventario di tutte le distanze o segmenti tra due punti della quadrettatura. Questi punti possono essere designati dalle loro coordinate da (0; 0) a (5; 5) se si sceglie il punto in una casella d'angolo della quadrettatura come origine delle coordinate (ad esempio, il centro della casella in alto a sinistra nelle Figure 1 e 2). (Ecco un esempio di questa lista, sotto forma di tabella, da completare con la guida dell'insegnante e la discussione di gruppo per le prime righe, poi individualmente.)
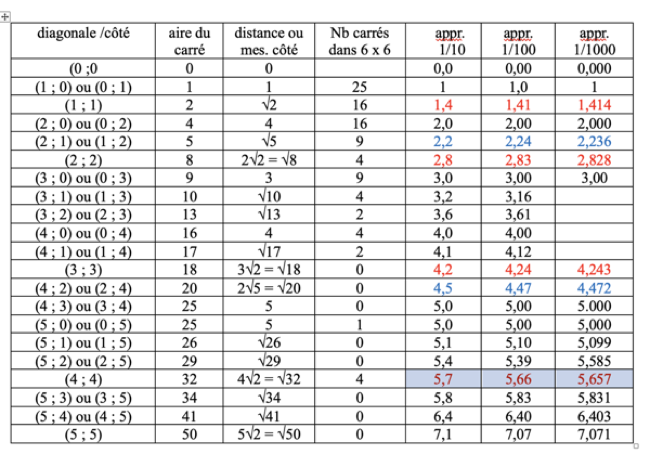
Tutto quello che dobbiamo sapere sulle lunghezze dei lati dei quadrati i cui vertici si trovano sui nodi di una griglia e sulle loro approssimazioni decimali.
d) Per chi conosce il teorema di Pytagora, questa è una buona occasione per avvicinarsi a una delle sue dimostrazioni.
In merito a tale problema, si veda anche:
Bernard Anselmo, Roberto Battisti, Paola Bajorko, Clara Bisso, Brunella Brogi, Fabio Brunelli, Federica Curreli, Speranza Dettori, Florence Falguères, Lucia Grugnetti, François Jaquet, Silvia Mazzucco, Bice Perna, Luciana Rapposelli, Elsa Renna, Patrizia Sabatini, Rosanna Sanna, M. Agostina Satta, Cinzia Utzeri, Vincenza Vannucci (2024).Percorsi didattici per la geometria piana con problemi RMT/Parcours didactiques pour la géométrie plane par des problèmes RMT. Gazzetta n. 14, pp. 75-112.