
Banca di problemi del RMT
gp6-it
 |
Banca di problemi del RMTgp6-it |
|
Trovare il lato dell’undicesimo e poi del centesimo quadrato di una successione di quadrati costruiti successivamente a partire dalle diagonali di ciascuno di essi.
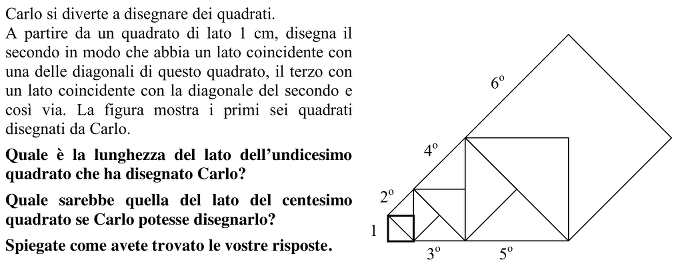
Osservare come sono formati i quadrati successivi: il primo, il terzo, il quinto, etc, cioè quelli di posto “dispari”, si susseguono nella stessa posizione del primo, mentre il secondo, il quarto, il sesto, etc., cioè quelli di posto pari, si susseguono nella stessa posizione del secondo, “obliquamente”. Per trovare la lunghezza del lato del 2° quadrato, calcolare la lunghezza della diagonale del primo e trovare quindi che misura 2 cm con il Teorema di Pitagora, oppure ricordarsi la relazione tra lato l e diagonale d di un quadrato: d=l 2 , a condizione di “accettare” che la scrittura “2 « sia il numero cercato e di non cercare di sostituirlo con un’approssimazione letta sulla calcolatrice come 1, 4142…
Si può anche trovare, nello stesso modo, la lunghezza della diagonale del 3° quadrato : 2 (in cm), poi quelle dei quadrati successivi : 22 per il 4°, 4 per il 5°, 42 per il 6° , 8 per il 7°, etc.
Comprendere allora che le misure delle lunghezze dei lati dei quadrati “dispari” sono in una progressione geometrica di ragione 2, di primo termine 1 (ovvero, la lunghezza del lato di un quadrato “dispari” di rango 2k + 1 è ottenuta moltiplicando 2 per se stesso k volte). Tenendo presente tale progressione, la lunghezza del lato dell’undicesimo quadrato si può esprimere come: 25 = 32 (in cm).
Osservare poi come si “comportano” i lati dei quadrati “pari”. In effetti capire che la successione delle misure delle lunghezze dei lati dei quadrati “pari” sono in progressione geometrica di ragione 2, di primo termine la lunghezza della diagonale del primo quadrato (ovvero, la lunghezza del lato di un quadrato di lato «pari» di rango 2k è ottenuta moltiplicando la lunghezza della diagonale del quadrato unitario per il prodotto di 2 per se stesso k-1 volte).
Infine, calcolare la lunghezza del lato del centesimo quadrato: 2 × 249 cm.
E’ anche possibile osservare le aree dei quadrati successivi scomponendoli in semi quadrati di forma triangolare e procedere con il conteggio senza far intervenire il teorema di Pitagora, né una scrittura letterale.
Il primo quadrato, di area 1 (in cm2) è composto da due triangoli, il secondo contiene 4 di tali triangoli e la sua area sarà dunque il doppio di quella della prima: 2 (in cm2); il terzo contiene 4 triangoli che sono semi quadrati del secondo, la sua area sarà allora il doppio di quella del secondo: 8 (in cm2) … e così di seguito, il 4° quadrato avrà un’area di 16, il 5° un’area di 32. La progressione è geometrica di ragione 2 con 1 come primo termine e permette di arrivare al termine generale mettendo in corrispondenza ciascun quadrato con la propria area e poi con la lunghezza del lato:
n. del quadrato 1 2 3 4 5 6 7 8 9 10 11 … 100 area (in cm2) 12 = 21 4 = 22 8 = 23 16=24 32=25 64=26 128=27 256=28 512=29 1024=210 … 299 lato (in cm) 1 √2 2 √8 4 √32 8 √128 16 √512 32 … √299
quadrato, diagonale, Pitagora, progressione geometrica
| Categoria | 0 | 1 | 2 | 3 | 4 | Nb.classi | Media |
|---|---|---|---|---|---|---|---|
| Cat 8 | 219 (49%) | 76 (17%) | 100 (22%) | 19 (4%) | 31 (7%) | 445 | 1.03 |
| Cat 9 | 71 (49%) | 17 (12%) | 36 (25%) | 12 (8%) | 8 (6%) | 144 | 1.09 |
| Cat 10 | 46 (42%) | 14 (13%) | 26 (24%) | 8 (7%) | 15 (14%) | 109 | 1.38 |
| Totale | 336 (48%) | 107 (15%) | 162 (23%) | 39 (6%) | 54 (8%) | 698 | 1.09 |
| Si ricorda che il problema è stato affrontato nelle condizioni particolari del RMT: intera classe, allievi in completa autonomia, da 5 a 7 problemi da risolvere, un solo foglio risposta per problema. | |||||||
Secondo i criteri dell’analisi a priori:
Errori legati ad un uso scorretto del teorema di Pitagora o all’impossibilità di scrivere il numero √2 in forma decimale limitata: incapacità di riconoscere la scrittura « √2 » come numero e talvolta incapacità di lavorare con approssimazioni (rilevate per esempio tramite la scrittura di tutte le cifre che appaiono sul display di una calcolatrice). Infatti, L’ostacolo contro il quale una parte degli allievi si scontra è quello legato al fatto di voler esprimere le lunghezze mediante un valore approssimato di 2 che richiede una grande quantità di calcoli.
Per la metà (49%) delle “incomprensioni del problema”, è possibile pensare ad un altro ostacolo: la perdita di senso e una sorta di “offuscamento” che impedisce un ritorno all’osservazione delle figure, alla loro scomposizione e ricomposizione in un ambito geometrico (si vedano le indicazioni didattiche).
Questo problema si presta bene alla mobilizzazione e alla gestione di diverse conoscenze. Le soluzioni richieste, infatti, implicano il ricorso alle proprietà di un quadrato, un uso ragionato del teorema di Pitagora, il riconoscimento della scrittura “√2” come numero, una buona gestione dell’approssimazione di un numero irrazionale, il riconoscimento di una progressione geometrica, vista così come uno strumento utile alla risoluzione di un problema di tipo “geometrico”. Infatti, sovente, si trattano in classe progressioni geometriche quasi esclusivamente in un registro numerico.
Vista la grande difficoltà del problema, rilevata dagli errori e dagli ostacoli segnalati in precedenza e dalle numerose “incomprensioni del problema”, è necessario trovare un altro approccio. Dopo qualche minuto di ricerca in gruppo, sovente infruttuosa, si potrebbe pensare, all’atto di una prima messa in comune, ad un approccio che vede un “va e vieni” tra l’ambito geometrico e quello numerico. In effetti, la struttura della progressione può essere perseguita tramite una manipolazione con una pavimentazione o illustrata con il disegno di triangoli (metodo purtroppo svalutato nella pratica scolare a partire dalla scuola secondaria). Per esempio, con 2 “mattonelle” triangolari si ricompone il primo quadrato, con 4 il secondo ... e si ottiene la successione 2; 4; 8; 16; … che si può continuare fino all’11° termine: 2048; poi considerare le aree in quadrati unità, poi i lati di questi quadrati per ottenere 32 cm..
Questa semplice manipolazione permette di rivisitare concetti che si pensa siano acquisiti ai livelli, 8, 9, 10, ma che possono o devono essere ancora consolidati: le conversioni di unità, l’origine geometrica della “radice quadrata”, la successione delle potenze di 2, la relazione fondamentale tra un quadrato e il quadrato costruiti sulla diagonale del primo, la scrittura “√2”, l’uguaglianza 12 + 12 = 2, … Ancora in fase di confronto dei risultati si può allora accordare la priorità all’ambito numerico: la successione dei numeri “relativi” a ciascun quadrato: c’è il numero della figura (numeri naturali 1, 2, 3, …), l’area (potenze di 2 a partire da 1; 2; 4; …), la misura dei lati che conduce a numeri irrazionali e alla loro espressione “√2”, eventualmente la misura delle diagonali. L’organizzazione di questi dati e la visibilità della loro corrispondenza assume un ruolo importante in questa prima parte numerica (si veda Compito per la risoluzione e saperi mobilizzati). I legami tra numeri successivi o tra numeri corrispondenti di due successioni possono allora essere messi in evidenza o addirittura “istituzionalizzati”. In questo caso, il passaggio da una scrittura come √512 a 16√2 è importante ma difficile per gli allievi, delicata da giustificare perché fa appello all’associatività e alla commutatività della moltiplicazione, una sorta di “distributività” dell’elevamento a quadrato (e dell’estrazione della radice quadrata) sulla moltiplicazione e a regole di semplificazione di scrittura (soppressione del segno “x”!
512 = 2 x 256 √512 = √(2 x 256) = √2 x √256 = √2 x 16 = 16 x √2 = 16√2
Viene infine il passaggio al concetto di progressione, con il suo numero illimitato di termini, che fa intervenire l’ambito algebrico e il termine generico del numero generico d’ordine n.
Per l’insegnante, è sufficiente aggiungere una colonna nella disposizione scelta per rappresentare il numero d’ordine o rango, le aree, i lati, ... e risolvere la questione. Per l’allievo si tratta di trovare una “formula” che funzioni per tutti gli esempi numerici già sistemati.
Il caso più semplice è quello dell’area, con un passaggio delicato da n a n – 1 che porta all’area del quadrato di rango n au moyen tramite l’espressione funzionale: n –––> 2n-1.
Per la misura del lato del quadrato, l’espressione diventa n –––> √(2n-1) che permette di ottenere √(299) o 249 √2 nel caso del centesimo quadrato.
Tutti gli altri ostacoli a proposito dell’interpretazione delle scritture, delle formule diverse per i quadrati di rango dispari o di rango pari, delle approssimazioni, delle proprietà elementari delle progressioni geometriche... richiederanno una parte più attiva nel dibattito da parte dell’insegnante.
Nel caso in cui il problema sia proposto in una classe del triennio di Scuola secondaria di secondo grado si possono utilizzare altre conoscenze; anzi, il problema potrebbe essere proposto proprio per favorire il consolidamento di conoscenze relative alla gestione di progressioni geometriche, magari proponendolo con il lato del primo quadrato di lunghezza l. Un possibile approccio potrebbe quindi essere il seguente:
Dopo aver calcolato il lato del decimo quadrato , rendersi conto che nelle decine successive, ogni lunghezza del lato del quadrato di ultimo indice dispari si ottiene moltiplicando la lunghezza dell’ultimo della decina precedente per e la lunghezza dell’ultimo di indice pari si ottiene moltiplicando ancora per . (Es: .
Ne consegue che essendoci 9 decine per giungere al 100-esimo posto, la lunghezza del lato del 99-esimo quadrato è , mentre la lunghezza
Bisso C., Grugnetti L., Maffini C., Marchini C., Rapuano M., Speroni A., Vannucci V. e ARMT. (2011) ‘Alla ricerca del segmento perduto’. Bologna: Pitagora Editrice.
(c) ARMT, 2010-2024