
Banca di problemi del RMT
gp7-it
 |
Banca di problemi del RMTgp7-it |
|
Dividere una griglia 4 x 4 (dove manca una delle caselle centrali) in cinque parti aventi stessa area e stessa forma, composte di quadrati interi.

Dividere una griglia di 4x4 (dove manca una delle caselle centrali) in cinque parti isometriche formate ciascuna da quadrati interi. Determinare il numero di quadrati di una parte (3) a partire dal numero dei quadrati disponibili (15), divisione per 5 o moltiplicazione con un termine mancante : 5x … = 15 o tentativi additivi di una somma di 5 termini uguali.
Determinare le diverse composizioni possibili dei tre quadrati (tre quadrati allineati o tre quadrati a forma di L).
Saper riconoscere le parti composte da tre quadrati nelle loro differenti posizioni :permanenza o invarianza delle figure geometriche attraverso traslazioni o rotazioni( la simmetria assiale o il ribaltamento non entrano in gioco visto che il pezzo ha un’asse di simmetria) .
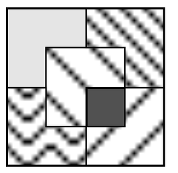
pavimentazione, superficie, area, isometrie, quadrato, equivalenza
Non ci sono dati statistici.
Il problema è sembrato semplice alle classi di cat.3 che l’hanno risolto. La ricerca è limitata a due forme : i tre quadrati allineati o i tre quadrati in forma di L.
Una volta che gli alunni si sono resi conto che la forma « 3 quadrati allineati » non conviene, tenuto conto della posizione del castello,essi cercano di pavimentare la superficie con la forma ad L.
Esempi di spiegazione:
Per trovare la soluzione abbiamo contato i quadretti del parco, meno il castello, erano 15 e lo spazio lo abbiamo diviso per 5, ci è venuto 3. Dato che nella cornice lungo i bordi c’erano 12 quadretti così 4 bambini avevano il loro spazio della stessa forma a L. Poi visto che ne avanzavano 3 al centro ed erano messi nella stessa forma abbiamo dato a tutti i bambini il loro spazio.
Vedendo il quadrato abbiamo contato i quadretti e diviso per tre pezzi in linea retta e poi una “elle”. Quindi non avevano la stessa forma. Poi abbiamo provato ad usare sempre la “elle” e siamo riusciti.
Si può utilizzare la ricerca esplicita del numero di pezzi con il conteggio dei 15 pezzi disponibili e una divisione per 5, per essere certi che i pezzi sono composti da tre quadretti. Poiché i quadretti possono anche essere interpretati come unità d’area, ci si situa allora in un approccio alle misure d’area.
In particolare il problema ben si presta ad essere utilizzato nelle classi per introdurre e/o sviluppare il concetto di equiestensione per somma. Inoltre l’attività consente di introdurre l’area in quanto grandezza prima di passare alle misure. Si evidenzia qui il legame fra superficie-pavimentazione e la grandezza area. Se la misura dell’area non è necessaria per la risoluzione del problema,il quadretto puo nondimeno essere considerato come unità d’area. Si situa allora in un approccio alle misure d’aree.
Il problema puo anche essere utilizzato in classe per lavorare sul riconoscimento di figure della stessa forma e delle medesima grandezza in posizioni differenti (spostamenti attraverso rotazione o traslazione).
- Proporre il medesimo problema sistemandoil castello in un angolo della griglia. In questo caso, la suddivisione è possibile utilizzando l’una o l’altra delle due composizioni dei 3 quadrati.
- Se il castello si trova su un altro quadrato, si potrebbe realizzare la suddivisione in 5 parti uguali aventi tutte la stessa forma (a L) ? Qualunque sia la posizione del castello, la suddivisione è sempre possibile attraverso la forma”3 quadrati a L”
- Dividere in 6 parti uguali un quadrato di 5x5 con una casella occupata dal castello, senza che le parti abbiano necessariamente la stessa forma. Questo problema permette di evidenziare l’equivalenza d’area di superfici con forme diverse.
Il problema Il parco del castello fa parte di una serie di problemi “isomorfi”, basati sul ricoprimento di una griglia quadrata con figure isometriche.
Per esempio:
Bisso C., Grugnetti L. (2006), « La costruzione del concetto di area con problemi del RMT », Gruppo di lavoro n° 6, “ellealquadrato”, in R. Battisti, R. Charnay, L. Grugnetti, F. Jaquet, D. Medici, M.-G. Rinaldi (Eds.) I problemi come supporto per l’apprendimento : il ruolo del RMT / Les problèmes au service de l’apprentissage : le rôle du RMT Parma 2006, ARMT, Dipartimento di Matematica dell’Università di Parma, Sezione ARMT di Parma, 169-187.
Bisso C., Grugnetti L. (2006), « Il ruolo dei problemi del RMT nella costruzione del concetto di area’, in L. Grugnetti, F. Jaquet, D. Medici, M. G. Rinaldi, I problemi del RMT nella didattica quotidiana/ les problèmes du RMT dans la pratique de la classe, Parma 2006, ARMT, Dipartimento di Matematica dell’Università di Parma, Sezione ARMT di Parma, 25-36
Douady R., Perrin-Glorian M.-J. (1989), « Un processus d’apprentissage du concept d’aie de surfaces planes », Educational Studies in Mathematics, 20, 387-424
ERMEL (2006), Apprentissages géométriques et résolution de problèmes au cycle 3, Ed. Hatier, Paris
Jaquet F. (2000), « Il conflitto aera-perimetro », L’educazione matematica, ed CRSEM, VI, 21, 2, (prima parte : n.2, 66-77, seconda parte : n.3, 126-143)
Rouche N. (1992), Le sens de la mesure, Formation Didier Hatier
(c) ARMT, 1999-2024