Il quadrato di Giuseppe

Identificazione

Rally: 19.F.16 ; categorie: 7, 8, 9, 10 ; ambiti: GP, GM
Famiglie:

• RD - Ricercare o utilizzare dimensioni
• RD/AP - Determinare aree e/o perimetri

Remarque et suggestion

Sunto

Determinare l’area delle 9 parti di un quadrato di 20 cm di lato determinato da quattro segmenti, paralleli due a due, ciascuno dei quali parte da un vertice e raggiunge il lato opposto alla distanza di un quarto di lato dal vertice.

Enunciato

Compito per la risoluzione e saperi mobilizzati

- Comprendere la costruzione della figura a partire dai dati, in particolare che le due parti in cui viene diviso ogni lato del quadrato misurano 5 e 15 centimetri.

- Riconoscere che i quattro triangoli rettangoli «grandi» (come ADF) hanno i cateti che misurano in cm 20 e 15, capire infatti che sono congruenti (il vertice dell’angolo retto di ciascuno di questi triangoli è uno dei vertici del quadrato e si passa da uno all’altro mediante un quarto di giro, un mezzo giro e tre quarti di giro.

- Le considerazioni precedenti dovrebbero convincere gli allievi che i due segmenti tracciati sono paralleli a due a due e perpendicolari a due a due.

- Quindi la figura al centro è un quadrato e le altre figure di cui si richiede l’area sono triangoli rettangoli e trapezi rettangoli.

- Riconoscere inoltre i due parallelogrammi congruenti, uno dei quali è BDGH.

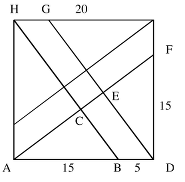
Le argomentazioni precedenti per stabilire che i segmenti tracciati sono a due a due perpendicolari o paralleli, così come altre dimostrazioni basate sulla congruenza o sulla similitudine di triangoli non sono qui richieste, vista l’età degli allievi e la diversità dei programmi.

Per il calcolo delle aree delle nove parti si possono seguire diverse procedure. Per esempio:

- Calcolare la misura dell’ipotenusa dei triangoli «grandi» con il teorema di Pitagora (riconoscere eventualmente la terna pitagorica 15, 20, 25): 25 centimetri, poi constatare che, conoscendo i lati di un parallelogramma 5 e 25 (in cm) e una delle sue altezze 20, si può determinare l’altezza relativa all’altro lato: (5×25): 20 = 4. Ciò permette di calcolare l’area del quadrato centrale, 16, quella dei quattro trapezi, (100 – 16): 2 = 42 e l’area dei quattro triangoli rettangoli «piccoli», [400 – (200 –16)] : 4 = 54 (tutto in cm²).

Oppure: dopo aver riconosciuto la similitudine fra i triangoli «piccoli» e i triangoli «grandi» mediante la congruenza degli angoli, calcolare con la proporzionalità (rapporti o proporzioni) le misure dei lati dei triangoli «piccoli» a partire da quelle dei triangoli «grandi» 25, 20, 15 → 15, 12, 9. Si ricavano quindi le aree dei  triangoli «piccoli»: (9 × 12): 2 = 54 (in cm2) e poi quella del quadrato al centro, togliendo dall’area del quadrato iniziale l’area dei quattro trapezi e quella dei quattro triangoli «piccoli»: 400 – [(4 x 42) + (4 x 54)] = 16 (in cm²).

Oppure: senza utilizzare la relazione di Pitagora, osservare che il triangolo “medio” è composto da un “triangolo piccolo” e da un trapezio rettangolo cosa che suggerisce una suddivisione in quattro strisce; procedere, quindi, attraverso la pavimentazione di un triangolo «piccolo» e di un triangolo «medio» per mezzo di triangoli unità aventi ipotenusa di 5 centimetri e quindi l’area del  triangolo «piccolo» è 9, l’area del trapezio, in grigio, è 7, l’area del triangolo grande è 9 + 7 + 9 = 25 (in triangoli unità) = 150 (in cm2),

Ciò permette di affermare che l’area di un triangolo unità vale 6 cm2 e quindi l’area dei triangoli «piccoli» è 54 e quella dei trapezi è 42 (in cm²).

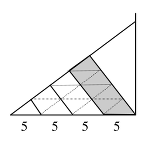
Oppure: fare un disegno preciso, in grandezza effettiva e dedurne le risposte tramite misure e calcoli, procedura che peraltro non è soddisfacente dal punto di vista matematico.

- Scrivere le risposte, in cm2 : 16 per il quadrato, 42 per i quattro trapezi e 54 per i quattro triangoli «piccoli»

Nozioni matematiche

triangoli, poligoni, teorema di Pitagora, congruenza, angolo, similitudine, deduzione

Risultati

19.F.16

Su 146 classes di 16 sezioni

Secondo i criteri dell’analisi a priori:

• 4 punti: Risposte corrette (16, 54, 42 in cm2) con i dettagli dei calcoli per ogni figura (le misure per i calcoli non sono trovati con semplice misura su un disegno)
• 3 punti: Risposte corrette con calcoli incompleti o non chiari o con misure prese direttamente su un disegno
• oppure un solo errore di calcolo con spiegazioni chiare e coerenti
• oppure due risposte corrette e ben spiegate
• 2 punti: Risposte corrette senza spiegazioni
• oppure due errori di calcolo con spiegazioni chiare e risposte coerenti
• oppure due risposte corrette con calcoli incompleti o non chiari
• 1 punto: Un sola risposta corretta
• oppure inizio di ragionamento corretto, con determinazione dell’ipotenusa dei triangoli «grandi» (25)
• 0 punto: Incomprensione del problema

(c) ARMT, 2011-2024