La terrazza di Giuseppe

Identificazione

Rally: 22.I.16 ; categorie: 7, 8, 9, 10 ; ambito: GP
Famiglia:

• LA - Utilizzare misure di lunghezze e aree

Remarque et suggestion

Sunto

Un quadrato di lato 10 m è diviso in nove parti da quattro segmenti che congiungono ogni vertice con il punto medio di un lato opposto. Determinare le aree delle parti dopo avere percepito la loro forma.

Enunciato

Compito per la risoluzione e saperi mobilizzati

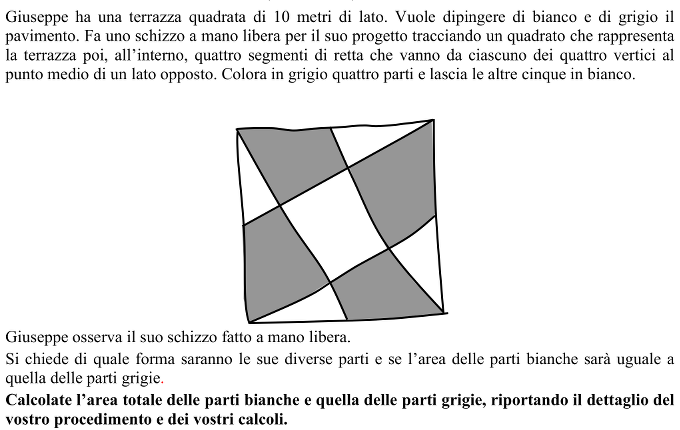
- Osservare il disegno, constatare che la figura si scompone in nove parti e rendersi conto che occorre determinare la forma di ogni parte prima di entrare nella fase del calcolo delle aree:

Questa determinazione può essere fatta ad occhio, ma deve essere confermata tramite un disegno preciso (con strumenti da disegno geometrico o su carta quadrettata) o giustificata da un’argomentazione dedotta dalle proprietà del quadrato e dei suoi lati suddivisi in due parti uguali dai punti medi.

Riconoscere che le nove parti sono un quadrato centrale, quattro trapezi rettangoli uguali e quattro triangoli rettangoli uguali. Si distinguono anche quattro triangoli “grandi” (figura 2) (composti da un trapezio e due triangoli “piccoli”) e quattro triangoli “medi” (figura 3) (composti da un trapezio e un triangolo “piccolo”). I triangoli “grandi” sono dei quarti del quadrato grande (misura dei cateti 5 e 10 cm, area 25 cm2, ipotenusa √125 o 5√5 cm).Tutti i triangoli sono simili fra loro (stessi angoli, e rapporto 2 tra i cateti) …

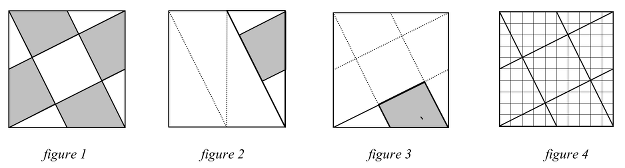
Passare infine al calcolo delle aree, con una delle numerose procedure possibili:

- tramite le misure delle lunghezze e il calcolo delle aree su un disegno “preciso” in scala, per esempio, su un quadrato di 10 cm di lato; mediante “quadrettatura” (costruzione precisa su carta a quadretti di un quadrato di 10 unità di lato e conteggio dei quadretti); mediante “pavimentazione” del quadrato in triangoli;; tramite scomposizione e ricomposizione

- per via algebrica: indicando con x e 2x le misure dei cateti del triangolo piccolo la cui ipotenusa misura 5 (in m), trarne x² + 4x² = 25 (Teorema di Pitagora), poi 5x2 = 25 e infine x² = 5 (in m²), che è anche l’area del triangolo (x 2x)/2 = x² .; …

I saperi mobilizzati, secondo le procedure utilizzate, ricoprono l’insieme dei programmi di geometria piana della scuola secondaria di primo grado: poligoni e calcolo della aree, isometrie, similitudini, relazioni metriche (teorema di Pitagora, Talete) oltre a potenze e radici quadrate, elementi di algebra.

Nozioni matematiche

geometria, quadrato, trapezio, triangolo, quadrilatero, area, omotetie, isometrie, rotazione, simmetria centrale, lato, vertice, punti medi, pavimentazione, similitudine, ipotenusa, teorema di Pitagora, algebra, equazione, disegno a mano libera

Risultati

22.I.16

Punteggi attribuiti, su 1245 elaborati di 14 sezioni

Secondo i criteri dell’analisi a priori:

• 4 punti: Risposta corretta completa (parti grigie 60 m2, parti bianche 40 m2) con spiegazioni complete delle operazioni effettuate e del modo in cui sono state riconosciute le figure (costruzione precisa, nomina di quadrato, triangoli e trapezi, o altra menzione esplicita della riflessione sulle forme…)
• 3 punti: Risposta corretta completa (60 m2 e 40 m2) con dettaglio dei calcoli delle aree (tramite pavimentazione, scomposizione, algebra, misura sul disegno, quadrettatura… ) ma senza alcuna menzione della riflessione sulla natura delle figure
• 2 punti: Risposta corretta completa (60 m2 e 40 m2) senza spiegazioni

    * oppure risposta vicina a 60 e 40 m2, dove i calcoli d’area sono effettuati su misure approssimative prese su un disegno 
    * oppure risposta completa e ben spiegata, ma sbagliata a causa d’un errore di calcolo 
1 punto:  Inizio di ragionamento corretto, per esempio calcolo dell’area solo per una delle parti (20 m2 per il quadrato, 5 m2 per un triangolo piccolo), con spiegazioni
    * oppure solamente un disegno preciso 
0 punto:  Incomprensione del problema

Procedure, ostacoli ed errori rilevati

Qualche osservazione provvisoria a partire dall’esame di qualche elaborato.

- La metà circa degli elaborati mostra una incapacità ad entrare in una risoluzione “con riflessione”: le aree grigie e bianche vengono dichiarate uguali; la somma delle due aree è lontana dal corrispondere a quella del quadrato originale (100); appaiono dei calcoli non corrispondenti alle misure prese; degli “scarabocchi” sembrano essre dei tentativi di ritaglio e riporto incoerenti; non vengono riconosciute le forme delle nove figure; …

- “L’inizio di ragionamento corretto” (punteggio 1) testimonia di una “entrata” nel problema, con riconoscimento del quadrato centrale, calcolo di aree di triangoli di cui uno dei lati misura 5 cm, …

- Tra le procedure che mostrano una comprensione del problema, una gran parte riposa su un disegno preciso della suddivisione del quadrato (in generale di 10 cm di lato) e le misure dei suoi vari segmenti. Tali procedure possono condurre a risposte lontane dalla soluzione «40 e 60» a seguito di errori di calcolo, oppure a risposte vicine alla soluzione dovute alle misure per forza di cose approssimative (ad esempio 38,72 e 58,96 quando la misura del lato del quadrato centrale è considerata come 4,4) senza il controllo della somma che dovrebbe essere 100 o ancora ad una prima area calcolata a partire da misure approssimative e la seconda calcolata come complemento 100.

L’ostacolo, in questo caso, è dovuto alla credenza secondo la quale la misura presa con il righello è la misura reale oppure alla non elaborazione del concetto di approssimazione.

- Le procedure per pavimentazione, ritaglio, compensazione che riposano sull’osservazione che il quadrato centrale equivale a quattro triangoli e che un trapezio equivale a tre triangoli cosa che conduce a suddividere il quadrato originale in cinque quadrati: due bianchi e tre grigi. Queste procedure non sono peraltro accompagnate da giustificazioni; le pavimentazioni o ritagli sono “evidenti” e riposano su un riconoscimento visivo.

- Si rileva anche frequenti calcoli della lunghezza di uno dei quattro segmenti tramite il teorema di Pitagora, che conduce all’approssimazione «11,8», ma non appare la scrittura 5√5 o √125 nei calcoli che seguono. Si tratta in questo caso dell’ostacolo legato alle scritture dei numeri irrazionali.

Indicazioni didattiche

La terrazza di Giuseppe è un problema “ricco” per la costruzione della conoscenze geometriche, ma evidentemente, visti i risultati ottenuti, “piuttosto difficile” per gli allievi dai 13 ai 16 anni nelle condizioni delle prove del RMT.

La varietà delle procedure di risoluzione osservate assicura l’interesse del loro confronto fra gli allievi, poi della loro istituzionalizzazione da parte dell’insegnante.

In particolare si può certamente approfittare per confrontare le procedure tramite le misure prese su un disegno, forzatamente approssimative anche se la costruzione è molto precisa, con le procedure per pavimentazione o scomposizione o ancora per via algebrica.

E’ anche possibile approcciare, secondo l’età degli allievi, la problematica della giustficazione con ragionamento deduttivo.

(c) ARMT, 2014-2024