La cinghia di Luca

Identificazione

Rally: 22.I.18 ; categorie: 9, 10 ; ambiti: GP, GM
Famiglie:

• ANG - Utilizzare angoli e/o misure di angoli
• ANG/CAL - Calcolare misure di angoli
• LA - Utilizzare misure di lunghezze e aree

Remarque et suggestion

Sunto

Trovare la misura del perimetro di una figura composta da due archi di circonferenze, di 3 e 15 cm di raggio, e da due segmenti tangenti alle due circonferenze, nel contesto di due ruote collegate da una cinghia di trasmissione. (E’ assegnato l’angolo di 60° formato dal segmento che collega i due centri e dal raggio della circonferenza maggiore congiungente il centro con uno dei punti di tangenza)

Enunciato

Compito per la risoluzione e saperi mobilizzati

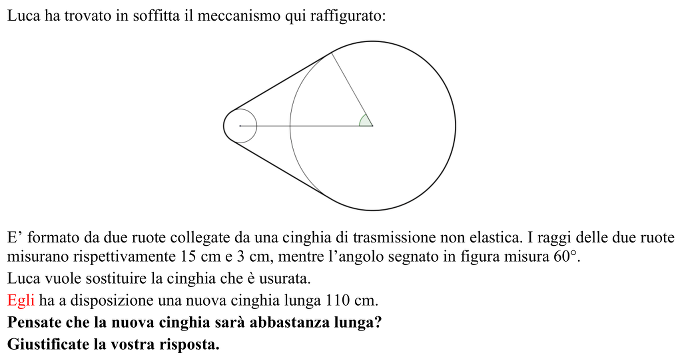
-Immaginare il dispositivo della cinghia e delle due ruote, poi passare alla figura geometrica “cinghia” composta da due segmenti e da due archi di cerchio. Analizzare questa figura e completarla al fine di ottenere della figure a proposito delle quali si dispone di conoscenze metriche: triangoli, rettangoli, parallelogrammi, trapezi, … Per esempio: tracciare dal centro del cerchio minore il segmento parallelo ad una delle tangenti, prolungare i due segmenti e il segmento che connette i due centri fino al loro punto di intersezione, …

- Riconoscere in queste “nuove” figure gli angoli retti, il parallelismo, isometrie (simmetrie), omotetie. Distinguere le misure note di lunghezza (3, 15) e di angoli (60, 90) da quelle che è possibile dedurre facilmente dalle altre (lunghezza degli archi) e da quelle che restano provvisoriamente incognite (fra le quali la lunghezza dei due segmenti).

- Impostare un’equazione che permette di ottenere la lunghezza dei due segmenti della cinghia.

Saperi mobilizzati: tangente, punto di contatto, perpendicolarità fra tangente e raggio dal congiungente il centro con il punto di tangenza, determinazione della lunghezza di un arco in funzione del “suo angolo” e del raggio, teorema di Pitagora, proprietà del semi triangolo equilatero, teorema di Talete, omotetia, similitudine, risoluzione di un’equazione di primo grado, arrotondamento di π o di √3.

Questi saperi dipendono evidentemente dalle figure scelte per la messa in relazione delle lunghezze da determinare. (Si veda la rubrica procedure, ostacoli ed errori rilevati)

Nozioni matematiche

geometria, circonferenza, lunghezza, arco, tangente, raggio, omotetia, angolo, perimetro, trapezio, triangolo, teorema di Pitagora, similitudine

Risultati

22.I.18

Punteggi attribuiti, sur 289 elaborati di 10 sezioni

Secondo i criteri dell’analisi a priori:

• 4 punti: Risposta corretta (no, la cinghia non è abbastanza lunga) con il dettaglio dei calcoli e con tutte le argomentazioni geometriche corrette
• 3 punti: Risposta corretta con il dettaglio dei calcoli che danno la lunghezza 22 π + 24√3, ma con spiegazioni incomplete
• 2 punti: Procedimento corretto, ma con un errore di calcolo che può anche portare a rispondere “sì”

    * oppure risposta incompleta: 22 π per gli archi o 24 √3 per i segmenti, senza effettuare i calcoli
    * oppure presenza di tutte le argomentazioni geometriche ma calcoli non terminati
1 punto:  Inizio di ragionamento corretto
0 punto:  Incomprensione del problema

Procedure, ostacoli ed errori rilevati

Il problema è risultato difficile, soprattutto per il calcolo dei segmenti di tangente BC e KH comuni alle due circonferenze e per il riconoscimento dell’arco di circonferenza BK della circonferenza minore. Queste difficoltà hanno portato nella maggior parte dei casi a interrompere il calcolo dopo la determinazione della lunghezza dell’arco HC. Chi ha continuato è incorso in due errori tipici:

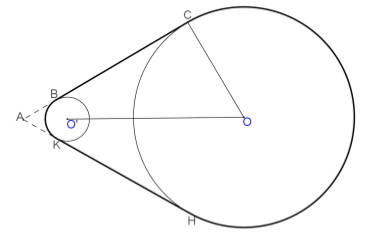
a. considerare l’arco BK come una semicirconferenza,

b. sostituire alla somma BC+BK+KH la somma AC+AH e dunque effettuare una approssimazione per eccesso.

La richiesta del problema e la conseguente necessità di approssimare il risultato della misura per confrontarlo con il valore 110 cm porta ad utilizzare fin da subito misure approssimate; la presenza di scritture simboliche con π o √3 è minima, anche nelle risoluzioni corrette. Si pensa che questa scelta sia, almeno in alcuni casi, consapevole.

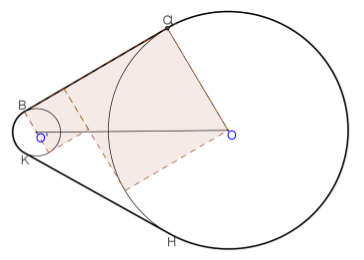
Si osserva in qualche elaborato, fra quelli analizzati, il tentativo di dedurre informazioni dalla figura come ad esempio “vedere” due quadrati, uno di lato il raggio della circonferenza maggiore e l’altro di lato il diametro della minore (si commette un piccolo errore in quanto il segmento BC risulta lungo 21 anziché 20,78)

Indicazioni didattiche

La cinghia di Luca è un “bel” problema dal punto di vista dell’insegnante, ma evidentemente, visti i risultati ottenuti, “troppo difficile” per allievi tra i 15 e i 16 anni nelle condizioni delle prove del RMT.

Ciò nondimeno le conoscenze necessarie alla risoluzione sono inserite nei programmi di geometria sia della secondaria di primo grado che in quella di secondo grado, inoltre nel biennio della scuola secondaria di secondo grado vengono affrontati solitamente problemi che necessitano di semplici procedure dimostrative e applicazioni di teoremi. L’analisi a posteriore del problema mostra che la loro gestione combinata e coordinata generalmente non è ancora possibile in genere a questa fascia di età (lo sarà forse a livello di triennio). Comunque alcuni gruppi di allievi (benché molto pochi) hanno risolto correttamente e con procedimento giustificato passo a passo.

Malgrado tutte queste riserve, il problema è interessante per la sintesi delle conoscenze geometriche e per un avvio ad una procedura scientifica che fa appello ad una grande varietà di saperi.

Per la sua utilizzazione in classe, è bene che venga conservato l’enunciato originale evitando di spezzettarlo in “piccoli passi” e che l'insegnante lasci spazio agli allievi nella proposta di procedure risolutive; è dunque necessario organizzare una gestione didattica che tenga conto della sua complessità: messe in comune successive a diversi livelli: appropriazione del dispositivo, analisi della figura “cinghia”, scoperta di figure accessorie interne,…

(c) ARMT, 2014-2024