Pavimento di legno

Identificazione

Rally: 23.I.14 ; categorie: 7, 8, 9, 10 ; ambito: GP
Famiglie:

• LA - Utilizzare misure di lunghezze e aree
• LA/UA - Gestire unità d’area
• RD - Ricercare o utilizzare dimensioni
• RD/AP - Determinare aree e/o perimetri

Remarque et suggestion

Sunto

Vengono dati il disegno di un pavimento rettangolare e il suo perimetro, fatto di listoni rettangolari di legno tutti uguali. Calcolare il prezzo dei listoni necessari per il pavimento conoscendo il loro prezzo al metro quadrato.

Enunciato

Compito per la risoluzione e saperi mobilizzati

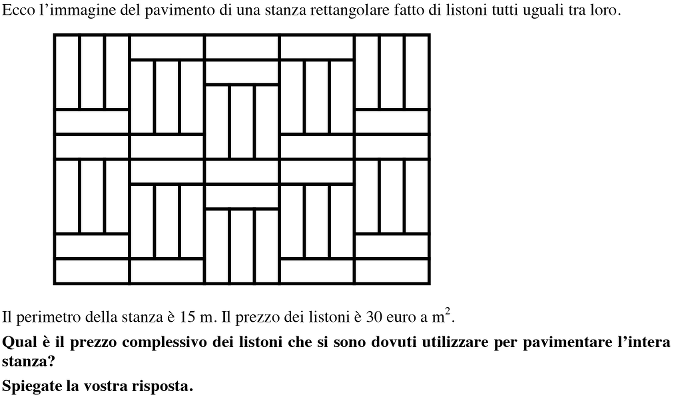
- Osservare la figura e coglierne le regolarità, dedotte dall’isometria dei rettangoli che compongono la pavimentazione: la lunghezza dei listoni è il triplo della larghezza e questa è la «relazione-chiave» della situazione, che suggerisce di prendere la larghezza di un listone come unità o di immaginare una trama quadrettata (quadrettatura) sulla quale è costruita la pavimentazione, con ogni rettangolo che ricopre 3 quadretti unità della trama.

- In questa percezione della trama o della larghezza di un listone come unità, le dimensioni della stanza sono 10 e 15 in lati di quadretti-unità, il perimetro è 50 = (10 + 15) × 2 in questa unità.

- Con la proporzionalità, in metri: 50 (in lati di quadretti-unità) ⇔ 15 (in m) determina il rapporto 15/50 oppure 3/10 o 0,3 e le dimensioni della stanza sono 3 e 4,5 (in m).

- Passare poi all’area del pavimento: 3 × 4,5 = 13,5 (in m2) e al prezzo dei listoni che è 13,5 × 30 = 405 (in euro).

Oppure, con una procedura algebrica, esprimere le dimensioni con delle lettere (per esempio x e y per la larghezza e la lunghezza dei listoni, poi sostituire y con 3x per arrivare all’equazione: 2(15x + 10x) = 15 poi 50x = 15).

Oppure misurare le dimensioni su un disegno, quello dell’enunciato e un altro realizzato rispettando i rapporti, calcolare il perimetro del pavimento sul disegno, dedurne la scala e determinare per proporzionalità le dimensioni reali del pavimento, poi calcolarne il prezzo.

Oppure procedere per tentativi.

Nozioni matematiche

rettangolo, perimetro, lunghezza, larghezza, area, unità, pavimentazione, prezzo, proporzionalità

Risultati

23.I.14

Su 1872 classi di 21 sezioni partecipanti alla prova I del 23° RMT,

Secondo i criteri dell’analisi a priori:

• 4 punti: Risposta corretta (405 euro) con spiegazioni complete (trasformazione di unità, dimensioni, area, prezzo)
• 3 punti: Risposta corretta con spiegazione incompleta
  oppure un solo errore di calcolo nella determinazione delle dimensioni dei listoni che comporta una risposta errata, ma coerente nella determinazione del costo della pavimentazione, con spiegazioni
• 2 punti: Risposta corretta senza spiegazioni
  oppure una risposta approssimata ricavata dalle misure di un disegno che rispetta i rapporti
  oppure le dimensioni della stanza sono calcolate correttamente, ma non è stato calcolato il prezzo per pavimentare la stanza
• 1 punto: Inizio di ragionamento corretto (esempio, il rapporto 3 tra le dimensioni dei listoni è menzionato)
  oppure scelta di dimensioni che non corrispondono alla figura, con tuttavia un perimetro di 15 m con un calcolo d’area e di prezzo coerenti con le dimensioni scelte
• 0 punto: Incomprensione del problema

Procedure, ostacoli ed errori rilevati

Su 83 elaborati analizzati (della Svizzera roamnda, categorie 7 e 8), si rilevano:

• 40 risposte corrette (405 euro)
• 23 risposte «375 euro»
• 5 risposte «500 euro»
• 15 risposte che vanno da 300 a 1500 euro.

(Da 4 a 2 punti sono stati attribuiti alle risposte corrette secondo la qualità delle spiegazioni)

Il 405 della risposta corretta può corrispondere solo ad un’area di 13,5 tramite la relazione 13,5 × 15 = 405 (nelle rispettive unità di misura). Di conseguenza le dimensioni del rettangolo sono state calcolate, in quel caso, correttamente con una scomposizione in unità comuni, la larghezza di un listone nella gran maggioranza dei casi, e un’applicazione opportuna della proporzionalità per passare da 50 (20 + 30) larghezza delle lame a 15 metri.

L’errore più frequente «375 euro», proviene da un’area di 12,5 m2 (12,5 × 15 = 375) la quale, a sua volta, proviene da una lunghezza del rettangolo di 5 m e una larghezza di 2,5 m menzionate esplicitamente nella gran parte degli elaborati corrispondenti, senza mai dare spiegazioni, talvolta con giustificazioni del tipo 5 + 2,5 = 7,5 e 7, 5 × 2 = 15 oppure 15 : 2 = 7,5 et 5 + 2,5 = 7,5.

Sembra che le dimensioni 5 m e 2,5 m siano state scelte dopo una stima visiva approssimativa.

Tra gli altri errori si trova sovente l’affermazione secondo la quale tre listoni (che formano dei quadrati sulla figura) hanno un’area di 1 m2, cosa che dovrebbe condurre logicamente alla risposta «500 euro», ma non è stata trovata nei 5 elaborati con tale risposta. Questa stima errata è stata in genere seguita da una ricostruzione di quadrati con gli altri listoni per arrivare ad aree comprese tra 15 e 18 «quadrati» e risposte tra 450 e 540 euro.

In sintesi, l’ostacolo centrale riguarda il rapporto 1 : 3 tra la larghezza e la lunghezza di un listone, che non è menzionato nell’enunciato, ma che deve essere percepito sul disegno vista la necessità di trovare una misura comune di lunghezza: la larghezza di un listone.

Indicazioni didattiche

L’interesse del problema risiede nella presa in considerazione del rapporto 1 : 3 tra la larghezza e la lunghezza di un listone che permette di trovare un’unità comune di lunghezza: (la larghezza di un listone). Il seguito della risoluzione viene svolta in maniera “lineare” facendo intervenire la relazione di proporzionalità che permette di passare dalle misure secondo l’unità comune alle dimensioni in metri, poi di effettuare il calcolo dell’area e quello del prezzo.

Si vedano anche i problemi La tavola da giardino et La scatola qui sont à l'origine du problème Il pavimento di Fabio.

(c) ARMT, 2015-2024