Numeri sconosciuti

Identificazione

Rally: 22.I.01, 06.I.03 ; categorie: 3, 4 ; ambito: NU
Famiglia:

• OR - Gestire una successione ordinata di codici

Remarque et suggestion

Sunto

Con 8 cifre date: 0; 7; 9; 3; 5 ; 8; 3; 6, formare quattro numeri di due cifre compresi tra 25 e 62, in modo tale che non vi siano coppie di numeri consecutivi

Enunciato

Compito per la risoluzione e saperi mobilizzati

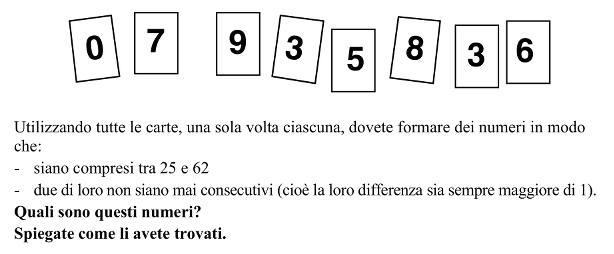
- Osservare le carte date, constatare che ce ne sono otto. Comprendere he queste carte possono formare dei numeri se le si dispone una accanto all'altra, che i numeri compresi tra 25 e 62, necessitano ciascuno di due carte. Dedurne che con le otto carte si potranno formare quattro numeri compresi tra 25 e 62. Questo primo compito esige dunque la «traduzione» delle carte in «elementi costitutivi di un numero» (o «cifre»), poi la presa di coscienza che i numeri tra 25 e 62 sono visualizzati per mezzo di due carte ciascuno.

- Si possono allora raggruppare le cifre (carte) due a due, per tentativi, poi procedere mediante controlli ed eliminazioni successive,

oppure: condurre una riflessione preventiva sulle cifre che potranno trovarsi nelle unità e quelle che potranno trovarsi nelle decine. Per esempio, constatare che lo 0 sarà nelle unità, così come le cifre 7, 8 e 9 e che si sono così suddivise le otto cifre in due gruppi: 3, 3, 5, 6 per le decine, 7, 8, 9, 0 per le unità. Il 6 dovrà allora essere associato allo 0 per non oltrepassare il 62, i due 3 al 7 e al 9 per non avere dei numeri consecutivi. Constatare che c’è un’unica associazione possibile: 37, 39, 58 e 60.

Tra queste due procedure, una per tentativi ed eliminazioni e l’altra per deduzioni logiche, c’è una grande varietà di procedimenti intermedi; le deduzioni logiche appaiono a mano a mano che si fanno dei tentativi.

I saperi mobilizzati sono quelli della numerazione: distinzione tra cifra e numero, conoscenza dei numeri di due cifre, di quelli compresi tra 25 e 62, distinzione tra cifre delle decine e delle unità.

Nozioni matematiche

numeri, numerazione, numerazione in base dieci, confronti, decine, unità, differenza

Risultati

22.I.01

Punteggi attribuiti su 848 elaborati di 15 sezioni

Secondo i criteri dell’analisi a priori:

• 4 punti: Scoperta dei quattro numeri (37, 39, 58, 60) con una spiegazione sul modo di scegliere le cifre delle decine e delle unità che conduce alla quasi certezza dell’unicità della soluzione. Per esempio, 7, 8 e 9 non possono essere le cifre delle decine perché i numeri sono inferiori a 62.
• 3 punti: Scoperta dei quattro numeri con una spiegazione che evidenzia una ricerca per tentativi con eliminazioni successive, ma che non permette di essere sicuri dell’unicità della soluzione. Esempio: “Abbiamo fatto dei tentativi a caso finché non abbiamo trovato questa soluzione”
  oppure i quattro numeri (38, 39, 57, 60) con una spiegazione completa (come per 4 punti), ma non ci si ricorda di constatare che 38 e 39 sono consecutivi
• 2 punti: Scoperta dei quattro numeri corretti, senza spiegazioni o con spiegazioni che non chiariscono procedura mentale seguita; per esempio, “abbiamo ritagliato i numeri e li abbiamo raggruppati a due a due”, oppure “abbiamo messo insieme i numeri dal più piccolo al più grande” …
  oppure i quattro numeri (37, 38, 59, 60) con una spiegazione completa (come per 4 punti), ma manca la constatazione che 37 e 38 e 59 e 60 sono consecutivi.
• 1 punto: Risposta con la presenza di più di quattro numeri (alcune cifre sono utilizzate più volte)
• 0 punto: Incomprensione del problema

Procedure, ostacoli ed errori rilevati

Qualche considerazione da una prima analisi a posteriori degli elaborati della Svizzera romanda:

- I criteri sono stati rispettati, con qualche precisione e complementi

- Un riferimento esplicito alle decine e unità, anche se non perfetto:

• 37, 39, 58, 60. I numeri grandi devono essere nelle u e i piccoli nelle d.

- E' stato rilevato, nell'ambito dei "3 punti", qualche esempio di spiegazione che però non permette di capire se gli allievi sono certi della unicità della loro soluzione:

• sapevamo che non poteva essere più grande di 62 e non più piccolo di 25, quindi abbiamo messo insieme i numeri abbiamo visto…
• … si sono utilizzati i numeri più grandi con i più piccoli, ma le cifre come 98 non vanno bene, perché sono più grandi di 62,
• … si sono trovati prendendo i più piccoli all’inizio e i più grandi alla fine.
• … si è andati per eliminazione
• Si sono tentate molte soluzioni e si è finito per trovare

- Tra i 14 elaborati che hanno avuto « 2 punti », se ne sono trovati 4 con numeri consecutivi e 7 che presentavano i quattro numeri ma accompagnate da « spiegazioni » che non sono tali:

• abbiamo preso per fare dei numeri
• abbiamo letto bene ll consegna , abbiamo guardato i numeri e abbiamo trovato
• abbiamo molto riflettuto e infine abbiamo trovato 39, 58, 37, 60
• 39, 58, 37, 60 li abbiamo trovati con la calcolatrice

- Qualche esempio per mostrare la varietà degli elaborati ai quali si è attribuito «1 punto» :

• Questi numeri sono 35, 38 e 60 e 109,
• 60, 37, 38, 59 o 30, 38, 57, 69, prima abbiamo trovato le cifre più piccole e poi le più grandi,
• 30, 33, 35, 37, 39 …57, 60 (ricerca esaustiva dei numeri tra 25 e 62, con una dimenticanza)
• Il risultato è 35, 39, 60. Noi abbiamo trovato solo questi numeri = 135

- Tra le « incomprensione del problema » (0 punti) ci sono evidentemente i fogli bianchi e il ricorso ad operazioni che denunciano una mancanza di senso :

- elaborati in cui si sono addizionati gli 8 numeri per trovare 41, come noi abbiamo fatto alla calcolatrice 7 + 0 + 9 …. = 41

- calcoli del tipo: 7 × 8 = 56 et 6 × 5 = 30 + 9 = 39

In generale i termini « cifre » et « numeri » non sono distinti tra loro e, talvolta, per i « 3 punti » si può fare l’ipotesi che i piccoli numeri presi per primi significa i piccoli numeri sono le cifre delle decine (le cifre delle decine vengono prima!)

Le analisi degli elaborati del Belgio confermano i risultati precedenti

Indicazioni didattiche

Il numero di insuccessi per un problema così semplice, a prima vista, mette in evidenza l’opportunità di riprendere le nozioni di « cifra » e « numero », spesso confusi tra loro : associare le carte alle « cifre », mostrare che esse permettono di rappresentare dei « numeri », che se ne prende una sola o che se ne mettono insieme di più, etc

Attività complementari :

- Rifare il problema modificando i numeri 25 e 62 .

- Proporre di fare l’elenco dei numeri di una cifra, di due cifre, di tre cifre, … che si potrebbero formare con le otto carte date. Cercare il numero più grande, il più piccolo, …

- …

(c) ARMT, 2014-2024