
Banca di problemi del RMT
nu21-it
 |
Banca di problemi del RMTnu21-it |
|
Contare tra i numeri da 1 a 100 quelli che si scrivono solamente con delle cifre “pari” o solamente con delle cifre “dispari”.
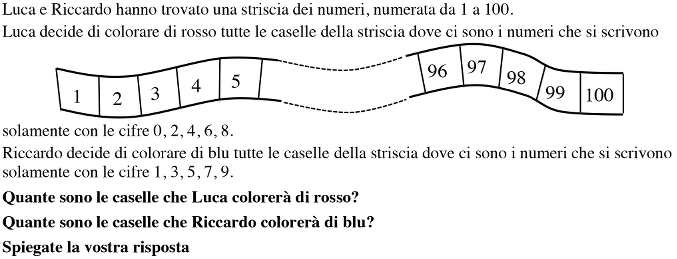
Interpretare la figura con il disegno parziale della striscia: considerarla come l’insieme dei cento numeri da 1 a 100 e non come una quindicina di caselle con i primi cinque numeri, gli ultimi cinque e uno spazio che permette di scriverne quattro o cinque da 6 a 9 o da 6 a 10.
Distinguere le parole “numero” e “cifra” e rendersi conto che ogni casella contiene un numero, ma che alcuni di questi numeri si scrivono con una cifra, altri con due cifre e un altro con tre cifre.
Distinguere le cifre 0, 2, 4, 6, 8 (“pari”) dalle cifre 1, 3, 5, 7, 9 (“dispari”) nei numeri per costatare che in certe caselle (o numeri) le cifre sono tutte “pari” e che bisognerà colorarle di rosso, in altre tutte “dispari” e saranno da colorare di blu o ancora che i numeri sono formati da due tipi di cifre e che le caselle che li contengono non saranno colorate.
Procedere al conteggio per rispondere alla domanda, tramite la scrittura e/o la coloritura delle caselle dei 100 numeri (o caselle) e conteggio uno a uno di ogni numero di Luca e di Riccardo, e trovare che Luca ha colorato di rosso 24 numeri (2 ; 4 ; 6 ; 8 ; 20 ; 22 ; 24 ; 26 ; … 80 ; 82 ; 84 ; 88) e Riccardo ha colorato di blu 30 numeri (1 ; 3 ; 5 ; 7 ; 9 ; 11 ; … 91 ; 93 ; 95 ; 97 ; 99).
numero, cifra, striscia, serie, numero naturale, numerazione
Punteggi attribuiti, su 1647 classi di 20 sezioni
| Categoria | 0 | 1 | 2 | 3 | 4 | Nb.classi | Media |
|---|---|---|---|---|---|---|---|
| Cat 3 | 379 (80%) | 33 (7%) | 21 (4%) | 6 (1%) | 33 (7%) | 472 | 0.48 |
| Cat 4 | 378 (63%) | 50 (8%) | 52 (9%) | 14 (2%) | 107 (18%) | 601 | 1.04 |
| Cat 5 | 314 (55%) | 50 (9%) | 68 (12%) | 21 (4%) | 121 (21%) | 574 | 1.28 |
| Totale | 1071 (65%) | 133 (8%) | 141 (9%) | 41 (2%) | 261 (16%) | 1647 | 0.96 |
| Si ricorda che il problema è stato affrontato nelle condizioni particolari del RMT: intera classe, allievi in completa autonomia, da 5 a 7 problemi da risolvere, un solo foglio risposta per problema. | |||||||
La tabella in alto permette di costatare che, nelle condizioni di somministrazione delle prove del RMT, la grande maggioranza dei gruppi di alunni, in particolare di categoria 3, non dà la risposta attesa e che solamente a partire dalla categoria 5 questa comincia ad apparire, soltanto nel 20% delle copie.
Il primo ostacolo è, evidentemente, la non distinzione tra “cifra” e “numero” alla lettura dell’enunciato. Anche se le parole “pari” e “dispari” non sono citate nel testo, per più della metà dei gruppi il compito è considerato come “colorare di rosso i numeri pari e di blu i numeri dispari” con la risposta “50 rossi e 50 blu”.
Il secondo ostacolo è l’interpretazione delle linee punteggiate della figura, per gli alunni di categoria 3 e a volte di categoria 4: la striscia è interpretata come limitata ad una quindicina di caselle, di cui è sufficiente completare le cinque o sei centrali. (Le linee punteggiate fanno parte delle convenzioni di scrittura (o di disegno) che appartengono al bagaglio culturale di un adulto, ma che i bambini non padroneggiano ancora.)
Al di là della confusione tra cifra e numero alla lettura, si può identificare un terzo ostacolo: la necessità di esaminare ogni numero, cifra per cifra, per rendersi conto che ci sono dei numeri di una, due o tre cifre nelle caselle della striscia, poi applicarci le condizioni di coloritura , in rosso, in blu o senza colore, per i numeri di due o tre cifre.
Le procedure rilevate dipendono dalla combinazione degli ostacoli di cui sopra, e da altri errori di conteggio.
- La risposta (50; 50) è determinata da un conteggio dei 100 numeri scritti e colorati in pari e dispari con degli errori del genere (50; 51), (49; 50), (47; 51) … a volte disposti in tabelle. Compare anche con delle operazioni come 100 : 2 = 50 oppure 50 + 50 = 100, …
- La risposta (5; 5) è ottenuta a partire dai dieci numeri scritti sulla striscia incompleta, suddivisi in pari e dispari; nel caso in cui la striscia sia stata completata con cinque o sei numeri, la risposta è adattata di conseguenza
- Quando i numeri sono analizzati cifra per cifra, appare la risposta corretta (25; 20), con qualche errore di conteggio quando tutti i numeri sono scritti e colorati parzialmente. Quando sono raggruppati in colonna e in tabelle, gli errori sono più rari.
- Si trovano anche risposte determinate dalla striscia incompleta, con l’analisi cifra per cifra, del tipo “cinque caselle blu: 1, 3, 5, 97, 99 e due caselle rosse: 2, 4”.
Nel momento di una ripresa del problema in classe, la confusione tra cifra e numero sarà dissipata rapidamente durante una discussione collettiva o grazie ad una spiegazione preliminare dell’insegnante che permetta di impegnare gli alunni in un procedimento corretto di analisi cifra per cifra.
L’interesse della ricerca consiste allora ad andare al di là della scrittura dei primi cento numeri, della coloritura e del conteggio che sono soltanto dei compiti “meccanici”. Delle procedure più sintetiche del semplice elenco devono permettere di evitare gli errori di conteggio e di fare ricorso a delle operazioni.
Per esempio, il raggruppamento per decine permette di distinguere i casi e di constatare che, per i numeri di due cifre, ci sono quattro decine la cui prima cifra è 2, 4, 6 oppure 8 e cinque la cui prima cifra è 1, 3, 5, 7, 9 ecc.
Per incitare gli alunni ad impegnarsi in questo genere di analisi, si può aumentare la lunghezza del nastro da esaminare. Per esempio: fare la ricerca sulle date di un calendario.
==== Ripostiglio ===
(c) ARMT, 2015-2024