
Banca di problemi del RMT
nu27-it
 |
Banca di problemi del RMTnu27-it |
|
Determinare un numero naturale n sapendo che per scrivere tutti i numeri naturali da 1 a n occorrono 672 cifre.
Analisi a priori:
- Capire che si vogliono numerare le case di una via utilizzando delle mattonelle su ognuna delle quali è scritta una cifra.
- Capire che occorre determinare l’ultimo numero civico sapendo che sono state utilizzate 672 mattonelle, cioè 672 cifre per scrivere tutti i numeri a partire da 1 fino all’ultimo numero della via.
- Capire che l’ultimo numero della via indica anche quanti sono in tutto i numeri civici.
- Procedere per tentativi, ipotizzando un possibile numero come ultimo numero della via. Ad esempio, ipotizzando che l’ultimo numero della via sia 50, calcolare la somma delle cifre che occorrono per scrivere i numeri da 1 a 50: 9 (numeri di una cifra) + 20 (10 numeri di due cifre fino a 19) + 20 (10 numeri di due cifre fino a 29) + 40 (20 numeri di due cifre fino a 49) +2 (cifre del numero ipotizzato come ultimo, cioè 50) = 91 cifre, troppo poche.
- Ipotizzare via via un numero più alto ed effettuare nuovamente il conto delle cifre che occorrono per scrivere tale numero e tutti i numeri a lui precedenti.
Si tratta di un processo lungo, in cui è abbastanza facile che vengano commessi degli errori di calcolo.
Oppure:
Organizzare una ricerca del conteggio delle cifre nella scrittura dei numeri, ad esempio
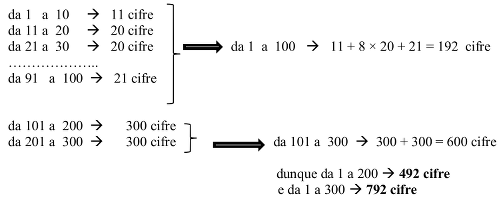
- Concludere che il numero cercato è compreso fra 201 e 300.
- Dedurre che bisogna effettuare la differenza 672 – 492 = 180 per calcolare il numero di cifre da aggiungere a 492.
Poiché in quell’intervallo i numeri sono formati da tre cifre, 180 : 3 = 60 è il numero da aggiungere a 200 per ottenere il totale di 672 cifre.
- Concludere che Via degli Olmi ha 260 numeri civici.
Oppure:
Procedere per sottrazioni successive:
Eseguire la somma 9 + 90 + 100 + 61 = 260 che è l’ultimo numero civico.
Oppure:
Procedere allo stesso modo per sottrazioni successive, considerando dapprima i numeri con una e con due cifre che contrassegnano le prime 99 case: 672−9 = 663; 663−180 = 483, restano 483 mattonelle da utilizzare; dividere tale numero per 3 per trovare che nella via ci sono 161 case contrassegnate da un numero di 3 cifre (483 : 3 = 161), aggiungere 99 a 161 e concludere che nella via ci sono 260 case (99 + 161 = 260).
Punteggi attribuiti su 175 classi di 17 sezioni:
| Categoria | 0 | 1 | 2 | 3 | 4 | Nb.classi | Media |
|---|---|---|---|---|---|---|---|
| Cat 6 | 23 (38%) | 15 (25%) | 10 (16%) | 5 (8%) | 8 (13%) | 61 | 1.34 |
| Cat 7 | 7 (12%) | 12 (21%) | 7 (12%) | 10 (17%) | 22 (38%) | 58 | 2.48 |
| Cat 8 | 10 (18%) | 11 (20%) | 3 (5%) | 9 (16%) | 23 (41%) | 56 | 2.43 |
| Totale | 40 (23%) | 38 (22%) | 20 (11%) | 24 (14%) | 53 (30%) | 175 | 2.07 |
| Si ricorda che il problema è stato affrontato nelle condizioni particolari del RMT: intera classe, allievi in completa autonomia, da 5 a 7 problemi da risolvere, un solo foglio risposta per problema. | |||||||
(c) ARMT, 2017-2024