Il nastro di Noe

Identificazione

Rally: 11.F.08 ; categorie: 5, 6 ; ambito: OPN
Famiglie:

• ADD - Cercare una somma o una differenza di numeri
• PRG - Gestire progressioni

Envoyer une remarque ou une suggestion

Sunto

Ricercare i numeri naturali consecutivi la cui somma è 105. Contesto: "striscia di numeri" o "sequenza di numeri naturali", con esempio: 34, 35, 36.

Enunciato

Compito per la risoluzione e saperi mobilizzati

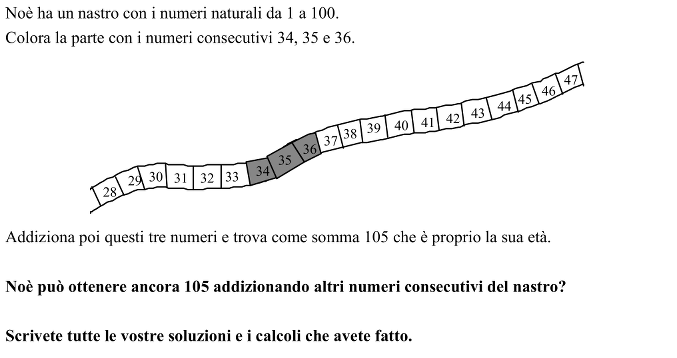
Analisi a priori:

- Appropriarsi delle due condizioni numeri consecutivi e somma 105.

- Immaginare che i numeri consecutivi e che danno come somma 105 possono essere in numero di due, oppure di tre o anche di più.

- Organizzare una ricerca di altri numeri che si susseguono oltre a quelli dell’esempio utilizzando anche la calcolatrice per tentativi o a caso,

oppure per tentativi organizzati cominciando con 2 numeri: 52 e 53 e continuando con 3 (quelli dell’esempio), con 4 (senza soluzione), con 5 (19, 20, 21, 22, 23), con 6 ( 15,16,17,18,19,20), con 7 (12, 13, 14, 15, 16, 17, 18), con 8 con 9(senza soluzione), con 10 (da 6 a 15), con 11, con 12, con 13 (senza soluzione), con 14 (1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14) che è l’ultima soluzione possibile in quanto la successione comincia con 1,

oppure cercare di addizionare i numeri di successioni che cominciano da 1 (funziona), poi da 2, da 3, da 4 ecc.,

oppure dividere 105 successivamente per 2, 3, ecc. e accettare quozienti interi che indicano il numero centrale se il divisore è dispari oppure "metà di interi", che indicano la media dei due centrali se il divisore è pari. (La calcolatrice è uno strumento essenziale per questa ricerche).

Nozioni matematiche

numerazione, addizione, divisione, divisori, media

Risultati

11.F.08

  Sulla la base di 72 classi partecipando alle finali regionali dell'11° RMT, da 13 sezioni.
Categoria
0
1
2
3
4
Nb.classi
Media
Cat 5
10 (26%)
6 (15%)
13 (33%)
5 (13%)
5 (13%)
39
1.72
Cat 6
8 (24%)
2 (6%)
6 (18%)
8 (24%)
9 (27%)
33
2.24
Totale
18 (25%)
8 (11%)
19 (26%)
13 (18%)
14 (19%)
72
1.96
Si ricorda che il problema è stato affrontato nelle condizioni particolari del RMT: intera classe, allievi in completa autonomia, da 5 a 7 problemi da risolvere, un solo foglio risposta per problema.
Secondi i criteri d'attribuzioni dei punteggi: 
4 points:  Le sette soluzioni o le sei nuove (34-35-36, puis 52-53 ; 19-20-21-22-23 ; 15-16-17-18-19-20 ; 12 à 18 ; 6 à 15 ; 1 à 14), con i calcoli corrispondenti
3 points:  Le sette soluzioni (o le sei nuove) senza calcoli o quattro o cinque nuove soluzioni con calcoli 
2 points:  Da quattro a cinque nuove soluzioni senza calcoli o da due a tre nuove con calcoli
1 point:  Una nuova soluzione con calcoli, oppure due o tre soluzioni senza calcoli, oppure soluzioni con errori di calcolo
0 point:  Incomprensione del problema
Per le 17 classi di cat. 5 e le 18 classi di cat. 6 esaminate durante la Finale Virtuale delle Finali, ovvero le classi vincitrici delle finali regionali, le medie sono leggermente più alte, rispettivamente 2,06 e 2,39.
Bibliografia
On trouve quelques données statistiques sur ce problème dans l’article sur la Finale des finales du 11e RMT in Actes des journées d’études sur le Rallye mathématique transalpin Vol. 4 Mondorf-les-Bains. (170-199) 
//
Jaquet. F. Le ruban de Noé. 2010. In Gazette de Transalpie 0 pp 43-48.