
Banca di problemi del RMT
op114-it
 |
Banca di problemi del RMTop114-it |
|
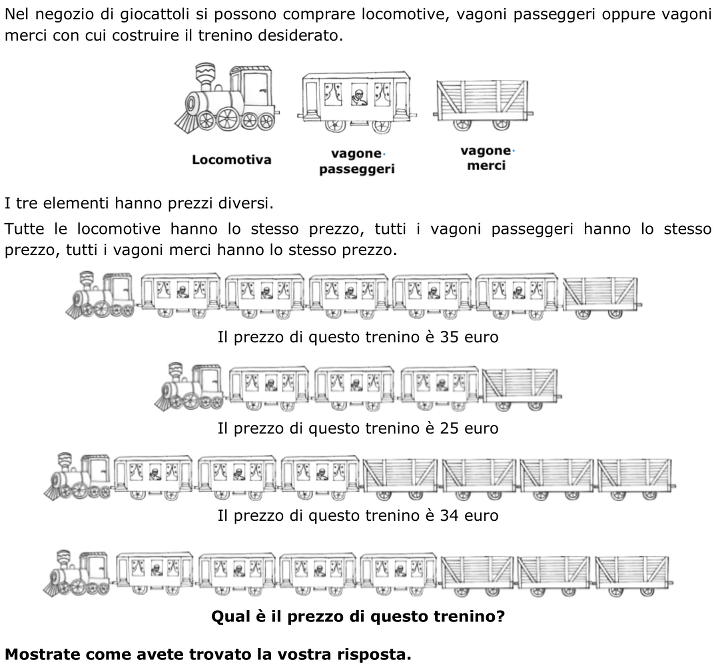
A partire da tre composizioni differenti, ottenute usando un certo numero di elementi di tre tipi diversi, e conoscendo il valore di ogni composizione, determinare il valore di una quarta composizione che contiene un numero diverso degli stessi elementi (L + 5P + M = 35 – L + 3P + M = 25 – L + 3P + 4M = 34 → L + 4P + 3M = ?)
Analisi a priori
- Capire che i tre elementi da cui è formato il treno hanno un costo diverso uno dall'altro e che elementi dello stesso tipo hanno lo stesso prezzo.
- Comprendere che la differenza di prezzo tra i trenini dipende dalla tipologia degli elementi utilizzati per comporli, dal loro numero e dal loro prezzo
- Osservare attentamente i disegni dei trenini e rendersi conto che il primo differisce dal secondo per due vagoni passeggeri, quindi la differenza di prezzo, 10 € (35 − 25), è da attribuire a questi due vagoni. Il prezzo di un vagone passeggeri sarà, allora, di 5 € (10 ÷ 2).
- In modo analogo, confrontando il secondo e il terzo trenino, osservare che differiscono per 3 vagoni merci e quindi la differenza di prezzo 9 € (34 − 25) è equivalente al prezzo di questi tre vagoni. Il prezzo di un vagone merci sarà, allora, di 3 € (9 ÷ 3).
Infine si può trovare il costo della locomotiva, a partire da uno qualsiasi dei treni di cui si conosce il prezzo, trovando il costo totale dei vagoni passeggeri e quello dei vagoni merci e togliendoli dal totale (treno 1: 35 - (5 × 5 + 3) = 7; treno 2: 25 - (5 × 3 + 3) = 7; treno 3: 40 - (3 × 5 + 6 × 3) = 7
- Calcolare il valore dell'ultimo treno: 7 (L) + 4 × 5 (VP) + 3 × 3 (VM) = 36 €
Oppure
- Una volta trovato il prezzo del vagone merci (3 €) e di quello passeggeri (5 €) nel modo descritto sopra, osservare che il trenino scelto da Andrea è come quello che costa 34 € con un vagone passeggeri al posto di un vagone merci e concludere che il trenino di Andrea costa quindi 2 € (5 − 3) in più, cioè 36 €
Oppure
- Procedere per tentativi più o meno organizzati assegnando un ipotetico valore ad un elemento e verificando di volta in volta la correttezza dell'ipotesi confrontandola con i prezzi conosciuti.
nombre naturel, addition, multiplication, équation,
Punti attribuiti, su 158 classi di 17 sezioni:
| Categoria | 0 | 1 | 2 | 3 | 4 | Nb.classi | Media |
|---|---|---|---|---|---|---|---|
| Cat 3 | 20 (40%) | 7 (14%) | 8 (16%) | 8 (16%) | 7 (14%) | 50 | 1.5 |
| Cat 4 | 10 (19%) | 6 (11%) | 9 (17%) | 12 (22%) | 17 (31%) | 54 | 2.37 |
| Cat 5 | 5 (9%) | 4 (7%) | 8 (15%) | 12 (22%) | 25 (46%) | 54 | 2.89 |
| Totale | 35 (22%) | 17 (11%) | 25 (16%) | 32 (20%) | 49 (31%) | 158 | 2.27 |
| Si ricorda che il problema è stato affrontato nelle condizioni particolari del RMT: intera classe, allievi in completa autonomia, da 5 a 7 problemi da risolvere, un solo foglio risposta per problema. | |||||||
Secondo i criteri determinati nell’analisi a priori:
(c) ARMT, 2018-2024