
Banque de problèmes du RMT
op141-fr
 |
Banque de problèmes du RMTop141-fr |
|
Envoyer une remarque ou une suggestion
Dans la table de division N × N, où les quotients sont écrits sous forme de nombres décimaux à deux décimales, reconnaître les quotients exacts, ceux qui seraient exacts s’ils étaient écrits avec trois décimales, ceux qui seraient exacts s’ils étaient écrits avec plus de trois décimales et ceux qui ne sont pas des nombres décimaux.

Analyse a priori:
- Observer la table, et la manière uniforme avec laquelle le programme affiche les résultats des divisions (toujours avec deux chiffres après la virgule, même si ce n’est pas nécessaire) et constater que la tâche consiste à distinguer les quotients exacts des approximations.
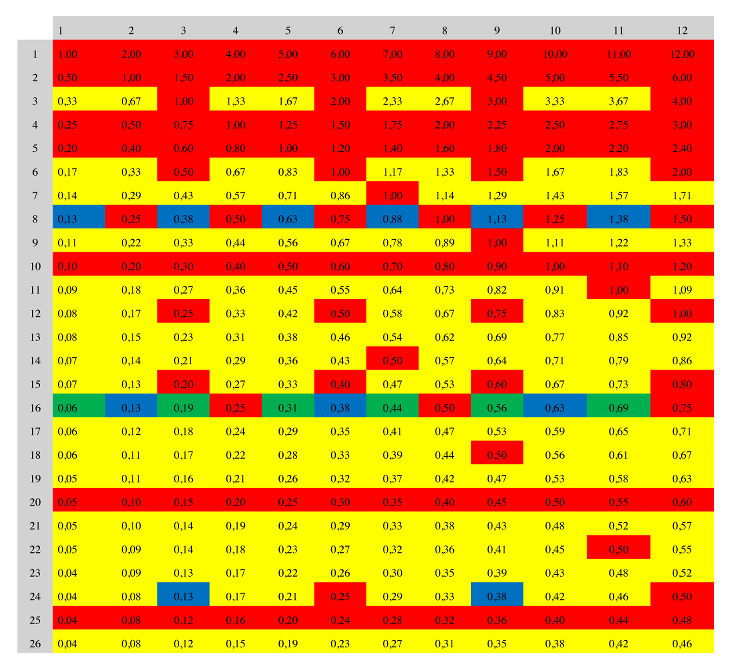
- Découvrir les très nombreuses régularités et les lier à l’opération de division. Par exemple les quotients de la première ligne sont les résultats de divisions par 1 donc des nombres naturels, ceux de la 2e ligne sont alternativement naturels ou se terminant par 5 comme premier chiffre après la virgule, ceux de la troisième ligne sont des nombres naturels (3/3, 6/3, 9/3, 12/3) ou des rationnels non décimaux …, ceux de la 16e sont des nombres décimaux : nombres avec deux chiffres après la virgule (4/16, 8/16 et 12/16), nombres avec trois chiffres après la virgule (2/16, 6/16 et 10/16) , nombres avec quatre chiffres après la virgule (1/16, 3/16, 5/16, 7/16, 9/16, 10/16 et 11/16 ) …
- On peut reconnaitre comme non décimaux (donc ayant un nombre illimité de décimales), les nombres qui sont égaux à des fractions dont le dénominateur, après simplification, ne se décompose pas uniquement avec 2 et 5 (par exemple 5/24 = 1/23 x 3, mais pas 6/24 = 1/4 = 1/22).

Il y a donc 178 cases coloriées en jaune (nombres non décimaux), puis 117 cases en rouge, 11 cases en bleu et, en dernier seulement 6 cases en vert (décimaux à plus de trois décimales, quatre en l’occurrence).
nombre, nombre rationnel, nombre décimal, division, simplification, fraction, fraction irréductible, quotient, quotient exact
Points attribués sur 1012 classes de 13 sections:
| Catégorie | 0 | 1 | 2 | 3 | 4 | Nb. de classes | Moyenne |
|---|---|---|---|---|---|---|---|
| Cat 8 | 426 (57%) | 167 (22%) | 77 (10%) | 37 (5%) | 37 (5%) | 744 | 0.78 |
| Cat 9 | 62 (48%) | 32 (25%) | 21 (16%) | 6 (5%) | 9 (7%) | 130 | 0.98 |
| Cat 10 | 65 (47%) | 29 (21%) | 18 (13%) | 7 (5%) | 19 (14%) | 138 | 1.17 |
| Total | 553 (55%) | 228 (23%) | 116 (11%) | 50 (5%) | 65 (6%) | 1012 | 0.86 |
| Rappel: Le problème est résolu dans les conditions particulières du RMT: classe entière, élèves en autonomie complète, 5 à 7 problèmes à résoudre, une seule feuille de réponses par problème. | |||||||
Les résultats ci-dessus sont éloquents: une grande majorité des élèves (et des adultes) ne savent pas ce qu'est une approximation décimale! (Les gens préféreront acheter un objet dont le prix affiché est 3,99 € que le même qui serait présenté au prix de 4 € car il leur paraît nettement moins cher !).
Les premières analyses a posteriori ont montré qu'il est inutile de chercher à identifier les erreurs ou à les juger. Elles sont trop nombreuses et varient d'une copie à l'autre. Le constat est que le concept d'approximation est encore à construire et que les obstacles sont élevés pour lire et écrire les nombres sous forme décimale.
Après l'introduction des nombres non entiers en sachant on entre dans une distinction délicate entre "discret" et "continu".
Il n'y a pas de miracle: il faut repartir des quotients de deux nombres naturels (ou entiers), revoir la division et son algorithme, écrire les quotients sous forme décimale, distinguer ceux qui ont un nombre fini de chiffres après la virgule de ceux qu'on ne peut pas écrire entièrement, découvrir la "période" d'un développement décimal illimité, ... Il faut ensuite expliquer les conventions d'écriture des approximations selon le nombre de chiffres après la virgule et observer comment les programmes de calcul (Exel par exemple) les appliquent.
Exemples d'activités en vue d'un parcours didactique avec la classe
À expérimenter en classe, selon des modalités déterminées par l'enseignant; avec envoi de description et commentaires pour rendre compte de l'opportunité de l'activité pour la construction des savoirs (notés en italique).