
Banca di problemi del RMT
op141-it
 |
Banca di problemi del RMTop141-it |
|
Envoyer une remarque ou une suggestion
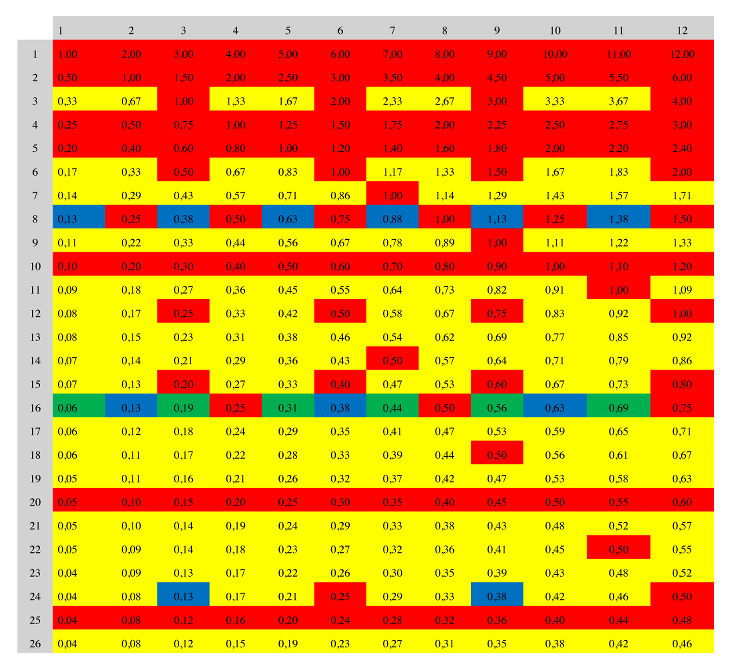
Nella tabella di divisione N×N, dove i quozienti sono scritti con due cifre decimali, riconoscere i quozienti esatti, quelli che sarebbero esatti se fossero scritti con tre cifre decimali, quelli che sarebbero esatti se fossero scritti con più di tre cifre decimali e quelli che non sono numeri decimali limitati.

- Osservare la tabella e il modo uniforme con il quale il programma indica i risultati delle divisioni (sempre con due cifre dopo la virgola, anche se non è necessario) e constatare che il compito consiste nel distinguere i quozienti esatti da quelli approssimati.
- Scoprire le numerose regolarità e metterle in relazione con l’operazione di divisione. Per esempio i quozienti della prima riga sono i risultati di divisioni per 1, dunque numeri naturali, quelli della seconda riga sono alternativamente naturali o terminano con 5 come prima cifra dopo la virgola, quelli della terza riga sono numeri naturali (3/3, 6/3, 9/3, 12/3) o numeri con infinite cifre decimali (periodici) …, quelli della sedicesima riga sono numeri decimali limitati (4/16, 8/16 e 12/16), numeri con tre cifre decimali (2/16, 6/16 e 10/16) e numeri con quattro cifre decimali (1/16, 3/16, 5/16, 7/16, 9/16, 10/16 e 11/16 ), …
- Si possono riconoscere come decimali non limitati i numeri periodici che corrispondono a frazioni i cui denominatori, dopo la semplificazione, contengono almeno un fattore diverso da 2 e 5 (ad esempio 5/24, ma non 6/24 che si semplifica in ¼).
- Un modo efficace di organizzare il calcolo è quello di lavorare riga per riga:

Ci sono pertanto 178 caselle colorate in giallo (numeri decimali illimitati), poi 117 caselle in rosso, 11 caselle in blu e, infine, solo 6 caselle in verde (decimali con più di tre cifre decimali, in particolare quattro):
numero, numero razionale, numero decimale, divisione, semplificazione, frazione, frazione irriducibile, quoziente, quoziente esatto
Punti attribuiti su 1012 classi di 13 sezioni:
| Categoria | 0 | 1 | 2 | 3 | 4 | Nb.classi | Media |
|---|---|---|---|---|---|---|---|
| Cat 8 | 426 (57%) | 167 (22%) | 77 (10%) | 37 (5%) | 37 (5%) | 744 | 0.78 |
| Cat 9 | 62 (48%) | 32 (25%) | 21 (16%) | 6 (5%) | 9 (7%) | 130 | 0.98 |
| Cat 10 | 65 (47%) | 29 (21%) | 18 (13%) | 7 (5%) | 19 (14%) | 138 | 1.17 |
| Totale | 553 (55%) | 228 (23%) | 116 (11%) | 50 (5%) | 65 (6%) | 1012 | 0.86 |
| Si ricorda che il problema è stato affrontato nelle condizioni particolari del RMT: intera classe, allievi in completa autonomia, da 5 a 7 problemi da risolvere, un solo foglio risposta per problema. | |||||||
I risultati parlano da soli: la stragrande maggioranza degli adulti (e degli adulti) non sa cosa sia un'approssimazione decimale! (Preferiremmo un articolo con un prezzo diverso da 3,99 €, mentre lo stesso prezzo qui sarebbe di 4 €, che è molto più caro!)
Le prime analisi a posteriori hanno dimostrato che è inutile cercare di identificare o giudicare gli errori. Ce ne sono troppi e variano da una copia all'altra. L'osservazione è che il concetto di approssimazione deve ancora essere sviluppato e che gli ostacoli alla lettura e alla scrittura dei numeri in forma decimale sono elevati.
Occorre ripartire dall’introduzione dei numeri non interi sapendo che si entra in una distinzione delicata legata al “conflitto” tra “discreto” e “continuo”.
Non esiste alcun miracolo: bisogna partire dai quozienti di due numeri naturali (o interi), riprendere la divisione e il suo algoritmo, scrivere i quozienti in forma decimale, distinguere quelli che hanno un numero finito di cifre dopo la virgola da quelli che non si possono scrivere per intero, scoprire il "periodo" di uno sviluppo decimale illimitato, ... Bisogna poi spiegare le convenzioni per scrivere le approssimazioni in base al numero di cifre dopo la virgola e osservare come le applicano i programmi di calcolo (ad esempio Excel).
Da sperimentare in classe, secondo le modalità stabilite dall'insegnante; con una descrizione e commenti per dimostrare la rilevanza dell'attività per la costruzione della conoscenza (indicati in corsivo).