
Banque de problèmes du RMT
op164-fr
 |
Banque de problèmes du RMTop164-fr |
|
Trouver un nombre (de gâteaux) correspondant à 3 petits récipients (plaques ou moules) sachant que 18 (gâteaux) correspond à un grand récipient et qu’un petit récipient contient la moitié (des gâteaux) du grand récipient.

L’appropriation du problème consiste à percevoir les deux grandeurs en jeu - les nombre de gâteaux et les dimensions des récipients (« plaques »), puis organiser et ordonner les données selon la description de l’énoncé. La lecture des deux phrases : « chaque petite plaque lui permettra de faire la moitié des gâteaux de la grande plaque » et « tous les gâteaux sont de même taille » doit permettre de comprendre que le nombre de gâteaux de chaque petite plaque est le même, (indépendamment de leur disposition), la moitié de 18, qui permettra de répondre à la question sur le nombre de gâteaux des trois petites plaques.
(Il faut relever à ce propos que la phrase « Simon veut faire des gâteaux de même taille avec trois petites plaques » figure dans le texte avant la phrase « une petite plaque permet de faire la moitié des gâteaux de la grand plaque » et incite à penser que la grande plaque est équivalente aux trois petites plaques dans un traitement « chronologique » des informations lues.)
Les savoirs mobilisé sont ceux d’un problèmes courant traité par passage à l’unité « sachant qu’il y a 18 objets dans 2 récipients, combien y en a-t-il dans 3 récipients de même contenance ? » : on cherche le nombre d’objets pour 1 récipient (9) puis on le répète trois fois ou on le multiplie par 3 pour trouver le nombre cherché
Le problème peut être aisément résolu sans faire appel aux opérations arithmétiques par un dessin des 18 gâteaux de la grande plaque (disposés par exemple en un rectangle de 3 x 6) répartis en deux parties (carrés de 3 x 3), puis par une nouvelle partie (carré de 3 x 3) et comptage du nombre total de gâteaux.
addition, soustraction, somme, multiplication lacunaire, associativité, commutativité
Points attribués, sur 1514 classes de 16 sections:
| Catégorie | 0 | 1 | 2 | 3 | 4 | Nb. de classes | Moyenne |
|---|---|---|---|---|---|---|---|
| Cat 3 | 136 (20%) | 80 (12%) | 33 (5%) | 148 (22%) | 287 (42%) | 684 | 2.54 |
| Cat 4 | 88 (11%) | 58 (7%) | 37 (4%) | 160 (19%) | 487 (59%) | 830 | 3.08 |
| Total | 224 (15%) | 138 (9%) | 70 (5%) | 308 (20%) | 774 (51%) | 1514 | 2.84 |
| Rappel: Le problème est résolu dans les conditions particulières du RMT: classe entière, élèves en autonomie complète, 5 à 7 problèmes à résoudre, une seule feuille de réponses par problème. | |||||||
(Version provisoire)
Globalement la réponse correcte (27) est trouvée par les trois quarts des classes, avec une progression significative de la catégorie 3 à la catégorie 4 Sur plus de 600 copies examinées, de cinq sections (CA, SI, SR, PR, RZ) c’est la procédure induite par l’énoncé : la moitié de 18 pour une petite plaque, puis 27 pour les trois petite plaques, qui a été relevée dans les trois quarts des cas.
Dans les autres cas, les élèves ont partagé les 18 gâteaux de la grande plaque en trois petites plaques de 6 gâteaux puis n’ont pas poursuivi la recherche de la solution qui les aurait ramené aux 18 gâteaux de départ. (selon l’information des « trois petites plaques » de l’énoncé qui précède celle de « la moitié » pour une petite plaque.)
Ce sont les observations écritures numériques qui s’avèrent intéressants car elles semblent caractéristiques de deux conceptions de la répartition des gâteaux. Pour l’adulte qui situe le problème dans le champ conceptuel de la multiplication et applique la propriété multiplicative de la proportionnalité, « la moitié » des 18 gâteaux se détermine par une division par 2 puis le nombre total des gâteaux des trois plaques par une multiplication par 3 :
18 : 2 = 9, puis 3 x 9 = 27
Dans une partie importante des copies, près de la moitié en catégorie 3, on voit cependant apparaître des écritures du champ conceptuel de l’addition : 9 + 9 = 18 puis 18 + 9 = 27 ou 9 + 9 + 9 = 27.
On se rend compte alors que pour ces élèves, trouver « la moitié » des 18 gâteaux de la grande plaque semble ressentie comme une réunion de deux parts égales qui constituent le tout. En écrivant 9 + 9 = 18, ils résolvent l’égalité lacunaire … + … = 18, en sachant bien que le seul nombre qui convient pour compléter l’égalité correctement est 9.
Cette remarque est à mettre en relation avec les observations de problèmes de recettes comme Gabrielle la petite sorcière (29.I.12, cat 6 - 8) où la perception additive de la relation entre deux grandeurs proportionnelles reste très majoritaire en catégories 5 et 6 avant d’être substituée par la perception de rapport de proportionnalité.
On a observé de nombreux dessins qui, en catégorie 3 surtout, ont sensiblement facilité la tâche de résolution, surtout lorsque les 18 objets de la grande plaque sont bien alignés, comme ici :
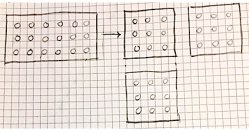
mais aussi même avec une représentation « contestable » :

Le problème n’a pas de grand intérêt pour une exploitation didactique en vue de la construction du concept de proportionnalité, vu la simplicité des relations en jeu sur de très petits nombres naturels. S’ils ne commettent pas l’erreur de lecture (considérer que les 18 gâteaux sont ceux des trois petites plaques, au lieu de deux), élèves ne peuvent pas « se tromper »
C’est au niveau des écritures et des représentations mentales des opérations qu’il pourrait être exploité : au sujet des liens entre addition, addition répétée et multiplication et des propriétés de ces opérations.
(c) ARMT, 2022-2024