
Banca di problemi del RMT
op180-it
 |
Banca di problemi del RMTop180-it |
|
Envoyer une remarque ou une suggestion
Trovare, seguendo le regole di un gioco, due somme di numeri da 1 a 10 tali che una valga 10 più dell’altra.
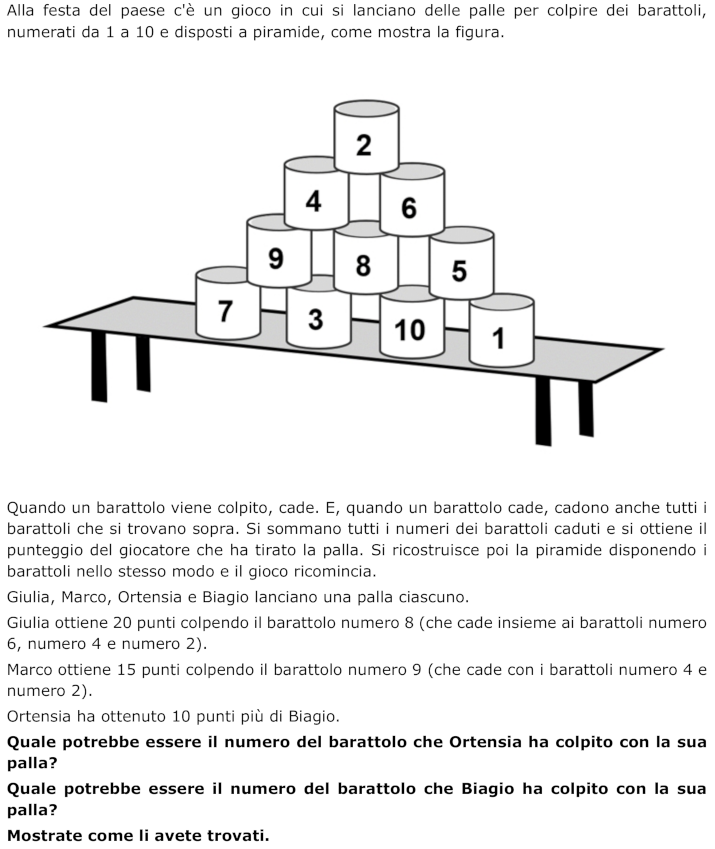
- Osservare gli esempi e comprendere come cadono i barattoli: quello che viene colpito trascina nella caduta non solo quello che è immediatamente sopra, ma anche quello che è appoggiato su questo e così via.
- Procedere per tentativi più o meno organizzati per trovare la soluzione. I barattoli 4 e 6 se colpiti fanno cadere solo il 2 e si ottengono le somme 6 e 8. Per i barattoli 8 e 9 si conosce già la somma. Con i barattoli che restano da colpire si ottengono le seguenti somme:
7 + 9 + 4 + 2 = 22
3 + 9 + 8 + 4 + 6 + 2 = 32
10 + 8 + 5 + 4 + 6 + 2 = 35
1 + 5 + 6 + 2 = 14
5 + 6 + 2 = 13
- Osservare, dai calcoli fatti, che solo colpendo i barattoli numero 7 e numero 3 si ottengono punteggi la cui differenza è 10 (32 – 22 = 10). Quindi, Biagio colpisce il barattolo numero 7 e Ortensia il barattolo numero 3.
addizione, numeri naturali, somma, combinazione
Punteggi attribuiti su 189 classi di 16 sezioni:
| Categoria | 0 | 1 | 2 | 3 | 4 | Nb.classi | Media |
|---|---|---|---|---|---|---|---|
| Cat 3 | 31 (51%) | 11 (18%) | 3 (5%) | 3 (5%) | 13 (21%) | 61 | 1.28 |
| Cat 4 | 18 (26%) | 12 (18%) | 9 (13%) | 10 (15%) | 19 (28%) | 68 | 2 |
| Cat 5 | 4 (7%) | 3 (5%) | 7 (12%) | 14 (23%) | 32 (53%) | 60 | 3.12 |
| Totale | 53 (28%) | 26 (14%) | 19 (10%) | 27 (14%) | 64 (34%) | 189 | 2.12 |
| Si ricorda che il problema è stato affrontato nelle condizioni particolari del RMT: intera classe, allievi in completa autonomia, da 5 a 7 problemi da risolvere, un solo foglio risposta per problema. | |||||||