
Banque de problèmes du RMT
op188-fr
 |
Banque de problèmes du RMTop188-fr |
|
Envoyer une remarque ou une suggestion
Décomposer 423 en une somme formée du plus grand nombre du termes égaux au 8e nombre triangulaire (36) et du minimum d'autres nombres triangulaires plus petits.
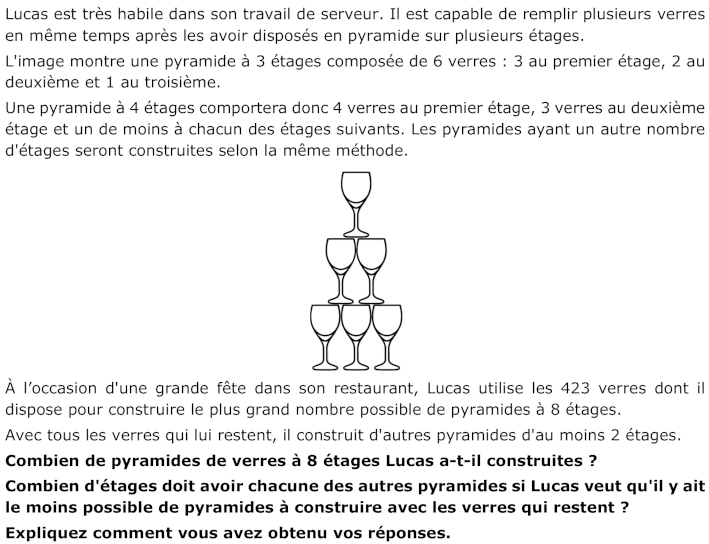
Appropriation
Comprendre la règle de construction des pyramides de verres: le premier étage d'une pyramide à 8 étages est constitué d'exactement 8 verres, le deuxième de 7 verres et ainsi de suite et que le nombre total de verres dans une pyramide à 8 étages est la somme des 8 premiers entiers naturels : 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 = 36.
Ou dessiner une pyramide de verres à 8 étages et comptez tous les verres (36).
Procédures
- Partir de 423 et soustraire plusieurs fois le nombre 36, en pointant le nombre de pyramides ainsi construites : (423 – 36 = 387 (une pyramide) ; 387 – 36 = 351 (deux pyramides) ; 351 – 36 = 315 (trois pyramides)) ... et continuer jusqu'à ce qu'il reste 27 verres.
- Ou additionner plusieurs fois 36 et se rendre compte qu'après avoir additionné 12 fois 36 on a obtenu un nombre supérieur à 423 soit 432 et qu'il faut donc s'arrêter à 396 (onze pyramides). Le reste est 423 – 396 = 27 (cette stratégie peut aussi s'effectuer par multiplication).
- Ou procéder en divisant 423 par 36 et trouver 11 avec un reste de 27. On peut donc construire 11 pyramides de 8 étages, chacune de 36 verres. On a donc utilisé 396 verres (36 x 1 = 396).
-Avec les 27 verres restants (423 – 96 = 27), il y a six possibilités. On peut construire : une pyramide à 6 étages (21 verres) et une pyramide à 3 étages (6 verres), ou une pyramide à 6 étages (21 verres) et deux pyramides à 2 étages (2 x 3 = 6 verres), ou une pyramide à 5 étages (15) et deux pyramides à 3 étages (2 x 6 = 12 verres), ou une pyramide à 5 étages (15) et quatre pyramides à 2 étages (4 x 3 = 12 verres), ou quatre pyramides à 3 étages (4 x 6 = 24 verres) et une pyramide à 2 étages (3 verres), ou neuf pyramides à 2 étages (9 x 3 = 27 verres). - Conclure qu'il y a 11 pyramides de 8 étages et qu'avec les verres restants, Luca construit une pyramide de 6 étages et une de 3 étages, qui est la seule possibilité respectant la contrainte « le moins possible de ». - On peut également procéder à l'aide d'un tableau, par exemple en observant que le nombre 27 est la somme des deux nombres triangulaires 10 et 21. - d) Procéder à l'aide d'un tableau, par exemple :
Étages 1er 2e 3e 4e 5e 6e 7e 8e Nombre total de verres utilisés 1 3 6 10 15 21 28 36
nombre naturel, nombre triangulaire, addition, somme, multiplication, produit, différence, division euclidienne
Points attribués, sur 222 classes de 20 sections:
| Catégorie | 0 | 1 | 2 | 3 | 4 | Nb. de classes | Moyenne |
|---|---|---|---|---|---|---|---|
| Cat 6 | 9 (12%) | 33 (44%) | 5 (7%) | 9 (12%) | 19 (25%) | 75 | 1.95 |
| Cat 7 | 4 (5%) | 23 (30%) | 14 (18%) | 3 (4%) | 32 (42%) | 76 | 2.47 |
| Cat 8 | 5 (7%) | 8 (11%) | 10 (14%) | 4 (6%) | 44 (62%) | 71 | 3.04 |
| Total | 18 (8%) | 64 (29%) | 29 (13%) | 16 (7%) | 95 (43%) | 222 | 2.48 |
| Rappel: Le problème est résolu dans les conditions particulières du RMT: classe entière, élèves en autonomie complète, 5 à 7 problèmes à résoudre, une seule feuille de réponses par problème. | |||||||