
Banca di problemi del RMT
op58-it
 |
Banca di problemi del RMTop58-it |
|
Envoyer une remarque ou une suggestion
Scoprire le regolarità di una griglia di numeri da un frammento che rappresenta le prime cinque righe e le prime 11 colonne, alla fine rendersi conto che è la tavola della moltiplicazione e completare altri quattro frammenti rettangolari (foto) da sei a dodici quadrati.
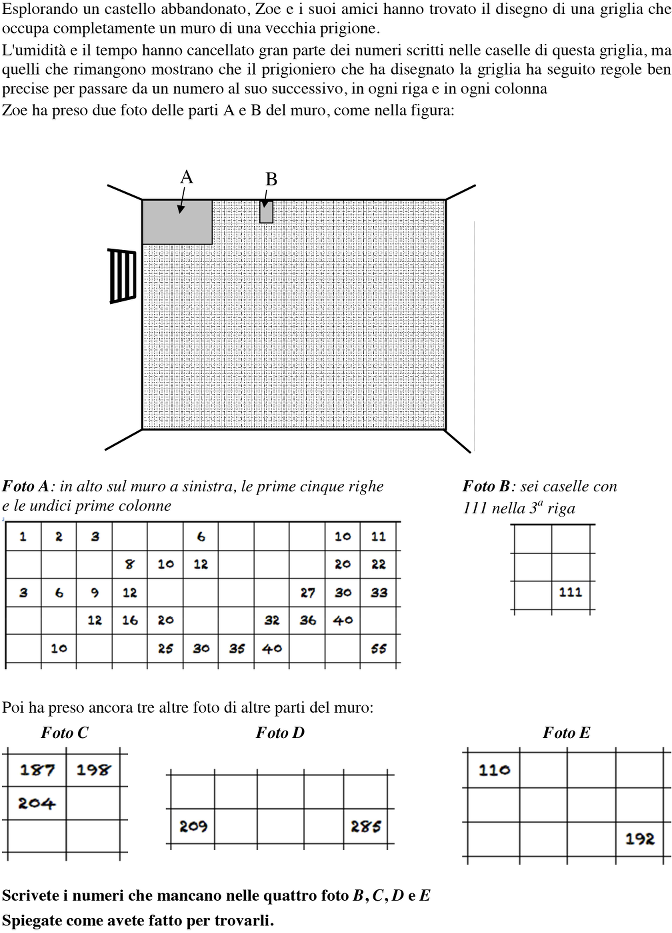
- Constatare, a partire dalla foto A, che la griglia dei numeri è costituita da sequenze con «regolarità già incontrate» nelle righe e nelle colonne e percepire che la griglia va trattata come «tavola di moltiplicazione»*, di cui ogni riga e ogni colonna sono costituite da multipli del primo numero (a sinistra, rispettivamente in alto).
- Per la foto B, rendersi conto che 111, sulla terza riga è il terzo multiplo del numero 37 (3 × ? = 111 o 111 : 3 = 37) e che la colonna precedente è quella dei multipli di 36.
- Per la foto C, 198 – 187 = 11 e 204 – 187 = 17, determinano la 11a riga e la 17a colonna.
- Per la foto D, 209 e 285 sono dei multipli di uno stesso numero, la loro differenza 285 – 209 = 76 vale quattro volte questo numero: 19 (76 : 4). Quindi i due numeri si situano sulla 19a riga. 209 = 19 × 11 si situa nella 11a colonna, 285 = 19 × 15 si situa nella 15a colonna.
- Per la foto E, si possono per esempio considerare i divisori di 110 (1; 2; 5; 10; 11; 22; 55; 110) e sapere che questo numero si può trovare nelle righe o colonne 1 e 110, 2 e 55, 5 e 22 o 10 e 11 poi, dopo qualche tentativo, trovare 5 per la colonna e 22 per la riga che corrispondono alla colonna 8 e alla riga 24 per 192.
Un altro modo è quello di cercare anche i divisori di 192 (1; 2; 3; 4; 6; 8; 12; 16; 24; 32; 48; 64; 96; 192) e di trovare delle coppie che differiscano di 2 per le righe: 22 e 24 e di 3 per le colonne: 5 e 8.
Riempire poi le quattro tabelle:

*Si tratta qui di una leggera forzatura al rigore matematico poiché teoricamente si potrebbero trovare altre funzioni oltre quella della tavola di moltiplicazione corrispondente ai numeri dati nella griglia, ma molto difficili da trovare.
numero naturale, addizione, progressione aritmetica, ragione della progressione, moltiplicazione, multiplo, divisore, tavola di moltiplicazione, riga, colonna, prodotto
Punteggi attribuiti 2198 elaborati di 21 sezioni:
| Categoria | 0 | 1 | 2 | 3 | 4 | Nb.classi | Media |
|---|---|---|---|---|---|---|---|
| Cat 6 | 679 (65%) | 194 (19%) | 106 (10%) | 45 (4%) | 23 (2%) | 1047 | 0.6 |
| Cat 7 | 405 (44%) | 171 (18%) | 139 (15%) | 128 (14%) | 82 (9%) | 925 | 1.26 |
| Cat 8 | 163 (25%) | 106 (16%) | 128 (20%) | 126 (20%) | 120 (19%) | 643 | 1.9 |
| Cat 9 | 27 (17%) | 9 (6%) | 33 (21%) | 33 (21%) | 57 (36%) | 159 | 2.53 |
| Cat 10 | 20 (14%) | 9 (6%) | 23 (16%) | 22 (15%) | 70 (49%) | 144 | 2.78 |
| Totale | 1294 (44%) | 489 (17%) | 429 (15%) | 354 (12%) | 352 (12%) | 2918 | 1.31 |
| Si ricorda che il problema è stato affrontato nelle condizioni particolari del RMT: intera classe, allievi in completa autonomia, da 5 a 7 problemi da risolvere, un solo foglio risposta per problema. | |||||||
I risultati seguenti sono tratti dall’analisi di 125 elaborati della Suisse Romande: 41 di categoria 6, 44 di categoria 7 e 40 di categoria 8.
Photo A
Sebbene le consegne non domandassero di completare le caselle vuote, gli allievi li hanno fatto, salvo qualche eccezione, e sempre correttamente, senza alcun errore. Siccome non dovevano spiegare come avessero trovato le loro risposte per questa prima ricostruzione, ci sono solo dei rari indizi su quello che hanno visto in questa prima foto: certi parlano di “tabelline”, altri di multipli, altri di sequenze logiche; qualche volta delle frecce indicano degli aumenti costanti tra i numeri di una progressione (+ 1, + 2, + 3, …), oppure di 1 da una riga alla seguente (+ 1).
Photo B
34%, 66% e 80% di risposte corrette secondo le rispettive categorie 6, 7 e 8.
Gran parte delle risposte sbagliate sono composte da numeri abbastanza vicini a 111 nelle cinque caselle da completare, tra cui numerosi multipli di 11.
Il numero 111 non è stato percepito come il terzo della sua colonna, sebbene l’enunciato precisi che si situa nella terza riga. Si può immaginare che questa “terza riga” sia stata considerata come quella della foto e non della griglia.
Photo C
29%, 70% e 80% di risposte corrette secondo le rispettive categorie 6, 7 e 8.
Nella grande maggioranza dei casi, gli allievi hanno percepito la differenza di 11 (198 – 187) per la prima riga e di 17 (204 – 187) per la prima colonna. Hanno così trovato 221 (204 + 17) come terzo numero della prima colonna, ma non hanno tenuto conto del cambiamento di ragione in seconda (12) e terza (13) riga e hanno aggiunto 11 ai numeri della seconda colonna, per ottenere 215 (204 + 11) e 232 (221 + 11) al posto di 216 e 234.
Queste risposte (66% in categoria 6) non fanno riferimento né alla moltiplicazione, né ai numeri delle righe e delle colonne; esse testimoniano solamente della percezione di “sequenze regolari con la stessa regola da una riga all’altra”.
Photo D
29%, 66% e 78 % di risposte corrette secondo le rispettive categorie 6, 7 e 8.
I risultati sono molto vicini , con uno scarto di qualche %, di quelli della foto C.
Le tre caselle vuote della seconda riga sono completate correttamente, 228, 247 e 266, nella grande maggioranza degli elaborati: la ragione della progressione, 19, è trovata a partire dalla differenza tra il primo e il quinto numero 285 – 209 = 76 e da una divisione per 4 (quattro scarti).
È sulla prima riga che si situano la maggioranza degli errori rilevati in questi elaborati: i numeri successivi di questa progressione differiscono anch’essi di 19 al posto di 18.
Malgrado la scoperta di 19, per la seconda riga della foto, gli alunni non hanno colto che si trattava della 19a riga della griglia e, di conseguenza, che la prima riga della foto è la 18a riga della griglia, né che 209 = 11 × 19 si situava nell’undicesima colonna della griglia, al di sotto di 198 (209 – 11).
La ripetizione delle addizioni nella progressione della seconda riga della foto non sembra aver spinto gli alunni a servirsi della moltiplicazione.
Photo E
7%, 39% e 55 % di risposte corrette secondo le categorie rispettive 6, 7 e 8.
È la più difficile delle quattro foto da completare. Non c’è nessun indizio che permetta di trovare la ragione di una delle progressioni e la soluzione passa obbligatoriamente attraverso la moltiplicazione (l’analisi dei prodotti).
I 42 gruppi che hanno completato correttamente questa griglia hanno tutti completato anche le foto C e D.
Ci possono essere diversi ostacoli che impediscono agli allievi di categoria 6 e 7 di completare le caselle della griglia numerica in questa foto. Saranno necessarie analisi più dettagliate, ulteriori sperimentazioni e interviste agli allievi per individuarli.
Nella rubrica "Per andare più lontano" vengono proposte alcune ipotesi riguardo le cause di questi ostacoli, di natura didattica (legati ai programmi e alle pratiche didattiche sulla tavola della moltiplicazione), di natura nozionale (analizzando le relazioni tra addizione e moltiplicazione) o di natura epistemica (in relazione al livello dell’allievo).
La tavola di moltiplicazione è il “cuore” dell’aritmetica dei numeri naturali; essa illustra tutte le proprietà dell’addizione e della moltiplicazione così come i legami tra le due operazioni.
Essa dovrebbe essere proposta sovente agli alunni, come oggetto di contemplazione, poi di osservazione attiva, per arrivare a delle “scoperte” che appaiono banali per l’adulto, ma che sono essenziali per il bambino. Per esempio:
C’è di che occupare, interessare, appassionare tutti quelli che entrano nel gioco della scoperta della tavola della moltiplicazione.
Esempi di attività per un percorso di apprendimento in classe
Da sperimentare in classe, secondo le modalità stabilite dall'insegnante; con una descrizione e commenti per dimostrare la rilevanza dell'attività per la costruzione della conoscenza (indicati in corsivo)
a) Chiedere a ogni allievo di costruire la propria tabella di moltiplicazione, che vada da almeno da 1 x 1 a 15 x 15, o meglio, a 20 x 20, o anche di più.
Scoprire che la tabella di moltiplicazione (tavola pitagorica) va oltre il 10 x 10 (o che le "tabelline" sono solo le prime righe e colonne) e che è composta da sequenze di numeri naturali di distanza costante 0, in termini operativi, che passiamo da un numero al successivo in ogni riga o colonna aggiungendo sempre lo stesso numero. Poi meravigliarsi di quante
b) Esplicitare il fatto che ogni riga e/o colonna della tabella contiene tutti i multipli del suo primo numero. Colorare righe e colonne può rendere visibili questi multipli, quindi i multipli comuni, ecc. Si possono anche suggerire altre "foto" oltre a quelle presenti nell'affermazione e/o chiedere agli studenti di crearne alcune da proporre ai loro compagni di classe.
Evidenziare multipli, progressioni aritmetiche, infinità di termini, ...
c) Utilizzare l'idea del problema Numeri in colore (31F.23) per stabilire la connessione tra il numero di divisori di un numero nella tabella di moltiplicazione e il numero di volte in cui compare nella tabella. In particolare, i numeri che compaiono solo due volte nella tabella di moltiplicazione sono importanti per l'aritmetica.
Concetto di divisore e di numero primo
d) Utilizzare l'idea del problema Le tabelline (19.II.05) per mostrare che le "tabelline" sono solo una parte molto piccola della tabella di moltiplicazione, l'idea del problema Croci sulla table (30.II.15) Croci sulla tabella (30.II.15) per scoprire una particolarità della somma di cinque numeri della tabella disposti "a croce". Osservare i numeri della diagonale grande della tabella e i loro due vicini (da sinistra in basso e da destra in alto) e cogliere l'occasione per verificare la scrittura letterale (n - 1)(n + 1) = n2 - 1; ...
Proprietà della tabella della moltiplicazione
e) Avvicinarsi alla "tabella delle divisioni", strettamente correlata alla precedente!! Decimali colorati (28.I.17)
Considerazioni storiche e didattiche
I differenti tipi di ostacoli che gli alunni incontrano nella percezione della tavola di moltiplicazione hanno diverse origini.
Istituzionalmente e socialmente la tavola di moltiplicazione è una referenza, legata ad una tradizione di valorizzazione delle conoscenze memorizzate, così come lo erano il catechismo, le eccezioni grammaticali, l’elenco delle capitali delle varie nazioni,… Dare una risposta immediata alla domanda “Quanto fa 7 per 8?” è stato a lungo considerato (e lo è ancora) come essere bravi in matematica. L’alunno lo sa perché riceve dalla sua famiglia e da quelli che lo circondano dei giudizi a proposito di questo tipo di competenza
Anche la scuola ha a lungo insistito sulla memorizzazione delle tabelline, consacrandoci un tempo importante dell’apprendimento della matematica. Questo obiettivo è sempre nei programmi scolastici, ma è stato spostato e scaglionato progressivamente da tutti i primi anni della scuola primaria verso gli ultimi tre anni.
Da un punto di vista nozionistico le tabelline non erano né una sequenza di coppie di numeri, né una sequenza di uguaglianze, ma solo la recita orale e scandita di gruppi di quattro parole: due per uno due , due per due quattro, due per tre sei,… La prima parola di ogni gruppo indicava il numero della tabellina e la seconda e la terza parola erano le “volte”, che variavano nell’ordine e andavano da 1 a 9 (o 10 , 12 secondo le epoche e le nazioni).
Le riforme dell’insegnamento della matematica di questi ultimi anni hanno evidentemente fatto evolvere le tabelline tradizionali e il modo di presentarle. Si parla di tabelline, ma legandole ad un numero “la tavola del 2”, si insiste meno sulla recita orale e si utilizzano sovente le sequenze di uguaglianza, sempre con uno dei fattori costanti e l’altro che varia nell’ordine, il lavoro di memorizzazione prende un aspetto più ludico.