
Banque de problèmes du RMT
op67-fr
 |
Banque de problèmes du RMTop67-fr |
|
Dénombrer une quantité d’objets représentés sur un dessin à partir de deux copies incomplètes de ce dessin, sur lesquelles figurent tous les objets, certains figurant sur une seule copie, d’autres sur les deux.
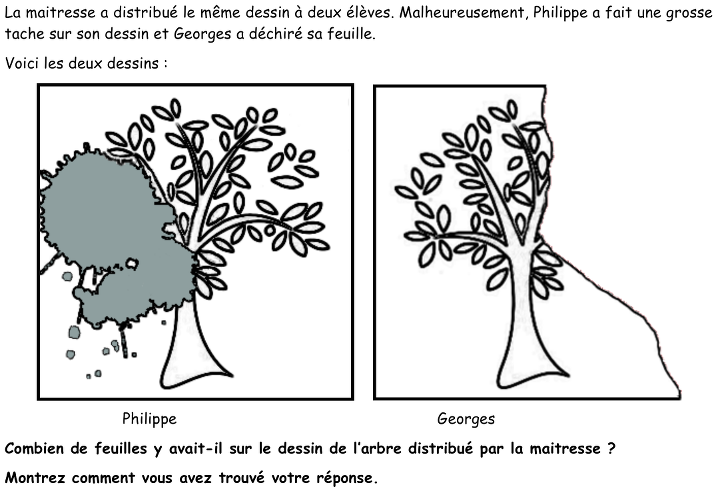
- Se rendre compte qu’il s’agit du même objet (un arbre dont il faut compter les feuilles) dont une partie est représentée sur chacun des dessins.
- Constater que toutes les feuilles ne sont pas visibles sur un seul dessin et qu’il faudra passer de l’un à l’autre pour les compter toutes en évitant de compter deux fois celles qui figurent sur les deux.
- Compter une à une les feuilles d’un dessin, puis celles de l’autre qui ne sont pas déjà comptées sur le premier. On peut s’aider de marques, d’une numérotation des feuilles, de couleurs, … pour ne pas en oublier. La difficulté principale est le contrôle des feuilles déjà présentes sur le premier dessin, qu’on peut éventuellement biffer une à une sur le second.
Ou, observer les dessins et constater que les feuilles peuvent être rangées dans 3 catégories :
Terminer en additionnant les trois nombres (20 + 20 + 28 = 68)
Ou reconstituer l’arbre entier soit en complétant un des deux dessins, soit en décalquant, soit encore en coupant et collant, après avoir identifié sur l’un des dessins la partie qui est manquante sur l’autre. Compter les feuilles de l'arbre reconstruit.
nombre naturel, addition, somme, soustraction, différence, comptage, dénombrement, exclusion
Points attribués, sur 1006 classes de 15 sections:
| Catégorie | 0 | 1 | 2 | 3 | 4 | Nb. de classes | Moyenne |
|---|---|---|---|---|---|---|---|
| Cat 3 | 122 (27%) | 66 (14%) | 44 (10%) | 74 (16%) | 150 (33%) | 456 | 2.14 |
| Cat 4 | 77 (14%) | 69 (13%) | 37 (7%) | 88 (16%) | 279 (51%) | 550 | 2.77 |
| Total | 199 (20%) | 135 (13%) | 81 (8%) | 162 (16%) | 429 (43%) | 1006 | 2.48 |
| Rappel: Le problème est résolu dans les conditions particulières du RMT: classe entière, élèves en autonomie complète, 5 à 7 problèmes à résoudre, une seule feuille de réponses par problème. | |||||||
Les observations qui suivent proviennent d’une première analyse de 83 copies de Suisse romande.
Les élèves qui ont résolu correctement le problème ont compté les feuilles. Une partie d’entre eux a commencé par celles visibles sur le dessin de Philippe (48) et ont ensuite ajouté les nouvelle feuilles du dessin de Georges (20) après avoir identifié celles qui sont en commun sur les deux dessins (20). Une autre partie des élèves a commencé par le dessin de Georges (40) et a ajouté les nouvelles feuilles de Philippe (28), toujours après avoir identifié celles qui sont en commun sur les deux dessins (20). Dans quelques copies, il semble toutefois qu’il y a une identification préalable des feuilles en trois parties: celles qui sont en commun, celles qui figurent seulement dans le dessin de Philippe et celle qui figurent seulement dans celui de Georges; suivi des comptages et de la somme des trois parties (20 + 20 + 48 = 68).
Les enfants se sont aidés de couleurs ou de marques pour repérer les feuilles au cours du comptage ou encore de découpages ou de décalquages. Une seule copie présente un début de numérotation de toutes les feuilles, abandonné ensuite parce que la procédure est trop longue. On observe plusieurs comptages après un regroupement des feuilles par 10.
Le problème a été résolu correctement par environ la moitié des élèves de catégorie 3 et les deux tiers de ceux de catégorie 4. C’est un problème qui peut être proposé en classe sans explications complémentaires et sans l’intervention de l’enseignant. Toute l’organisation de la recherche doit être laissée à la charge des élèves.
Il peut être intéressant d’identifier la partie commune des deux dessins qui ne doit être comptée qu’une seule fois au cas dans l’addition.
La comparaison des différentes stratégies de résolution peut faire apparaître qu’une partition par groupes de 10 économise du temps et simplifie le dénombrement.
(c) ARMT, 2016-2024