
Banca di problemi del RMT
pr17-it
 |
Banca di problemi del RMTpr17-it |
|
Trovare i numeri di due tipi di motivi disposti a scacchiera, che decorano un rettangolo quadrettato (tappeto) di 680 cm per 440 cm e dove 7 colonne complete, di 11 quadrati sulla larghezza, sono visibili. (Dopo aver determinato il numero di colonne nella lunghezza).
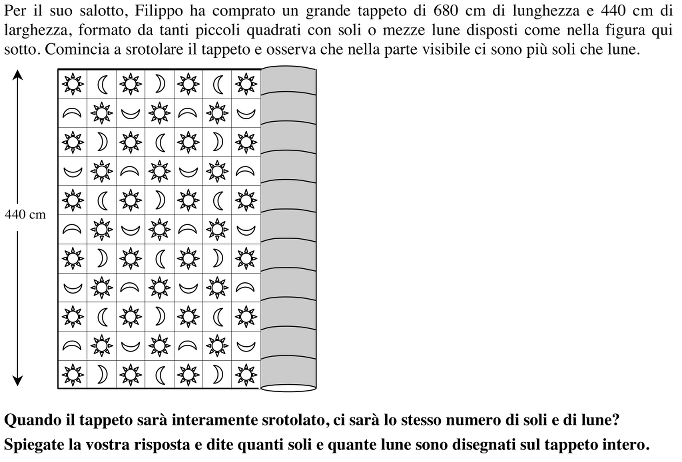
Sur la figure, trouver le nombre de soleils (39) et de lunes (38), en tenant compte de la régularité dans leur disposition (pour les soleils : 5 dans les colonnes paires et 6 dans les colonnes impaires ; pour les lunes : 6 dans les colonnes paires et 5 dans les colonnes impaires).
Trouver ensuite le nombre de colonnes sur la longueur du tapis par proportionnalité :
Compter qu’il y a 11 lignes (ou carrés) dans la largeur de 440 cm, et trouver le nombre de carrés dans la longueur de 680 cm (la mesure du côté du carré, identique dans les deux dimensions, correspond au rapport de proportionnalité). La mesure du côté d'un carré est 440 : 11 = 40 (en cm), le nombre de colonnes est 680 : 40 = 17.
A partir de là, trouver le nombre de soleils et de lunes sur le tapis de 8 colonnes paires et 9 colonnes impaires :
- soleils : 8 × 5 + 9 × 6 = 94 - lunes : 8 × 6 + 9 × 5 = 93
Rédiger la réponse : « plus de soleils, 94, que de lunes, 93 » et les explications.
Les savoirs mobilisés sont : le dénombrement par comptage ; la distinction pair / impair ; la reconnaissance d’une relation (de proportionnalité) entre les dimensions du rectangle (largeur et longueur) et les nombres de carrés correspondants sur ces côtés ; les opérations d’addition, multiplication, division sur des nombres entiers inférieurs à 200 (pour le calcul de la « 4e proportionnelle et celui des nombres totaux de motifs) ; l’isométrie des côtés d’un carré (pour déterminer le coefficient de proportionnalité).
multiplication, division, proportionnalité, quatrième proportionnelle, linéarité, rectangle, quadrillage
20 sezioni
| Categoria | 0 | 1 | 2 | 3 | 4 | Nb.classi | Media |
|---|---|---|---|---|---|---|---|
| Cat 5 | 305 (59%) | 61 (12%) | 40 (8%) | 35 (7%) | 76 (15%) | 517 | 1.06 |
| Cat 6 | 401 (49%) | 121 (15%) | 60 (7%) | 79 (10%) | 160 (19%) | 821 | 1.36 |
| Cat 7 | 187 (27%) | 112 (16%) | 57 (8%) | 92 (13%) | 234 (34%) | 682 | 2.11 |
| Totale | 893 (44%) | 294 (15%) | 157 (8%) | 206 (10%) | 470 (23%) | 2020 | 1.54 |
| Si ricorda che il problema è stato affrontato nelle condizioni particolari del RMT: intera classe, allievi in completa autonomia, da 5 a 7 problemi da risolvere, un solo foglio risposta per problema. | |||||||
Secondo i criteri dell’analisi a priori:
Procedure efficace
Le classi con la risposta giusta hanno fatto il primo passo per determinare che un quadrato è di 40 cm quadrati e che ci sono 17 colonne. Alcune classi hanno inoltre determinato il numero totale di quadrati (187). Il numero 17 è stato determinato dividendo 680 per 40 o trovando il numero che moltiplicato per 40 dà 680 (moltiplicazione con fori o prove e regolazioni del prodotto).
Quindi, le classi di categoria 5 e 6 spesso procedono disegnando l'intero tappeto e contando i motivi.
Nelle categorie 6 e 7, il supporto su un disegno è ancora molto presente, ma il conteggio dei motivi viene effettuato mediante un calcolo (addizione, moltiplicazione).
Dalla categoria 6, vediamo il ragionamento basato sul fatto che ci sono più (una in più) colonne dispari rispetto alle colonne pari, con il calcolo del numero di soli e lune.
Appare anche (ma raramente e al livello 7), un ragionamento basato sul fatto che una "colonna pari compensa una colonna dispari" e che, poiché esiste un'altra colonna dispari, il numero di soli supera di 1 il numero lune.
Errori
La stragrande maggioranza delle risposte errate (tutti i livelli combinati) apparentemente proviene da un malinteso sul problema, alcuni numeri che appaiono nelle soluzioni sono comunque difficili da interpretare.
Un errore che appare più volte è dovuto al fatto che gli alunni hanno ritenuto che il tappeto totale avesse una lunghezza doppia rispetto a quello del disegno (probabilmente in relazione al fatto che la parte disegnata del tappeto occupa circa la metà larghezza della pagina).
Questo problema, nella sua versione attuale, sembra inadatto per iniziare il lavoro sulla proporzionalità. Qui, nessuno studente ha utilizzato il fatto che, conoscendo il numero di lune e soli su 2 colonne e tenendo conto delle regolarità, è possibile dedurre il numero di ogni tipo di elemento su 16 colonne (8 volte di più ) e quindi su 17 colonne. Ciò può anche essere spiegato dal fatto che non esiste una relazione semplice tra la lunghezza visibile del tappeto (280 cm) e la sua lunghezza totale (680 cm) o persino la lunghezza invisibile (400 cm). Tuttavia, la proporzionalità avrebbe potuto essere mobilitata se gli studenti avessero fatto affidamento sul fatto che il numero di modelli di ciascun tipo viene ripetuto prendendo le colonne due per due: dopo aver identificato che ci sono 11 lune e 11 soli le prime 2 colonne, possiamo dedurre che ci sono 8 volte più disegni su 16 colonne (quindi 88 di ogni tipo) e che è quindi sufficiente aggiungere il numero di disegni nella 17a colonna.
D'altra parte, questo problema è più adatto a lavorare con un approccio di tipo "concatenamento all'indietro" o "analisi ascendente", quest'ultimo consistente, dalla domanda per determinare ciò che è necessario sapere per rispondere: qui, la domanda porta a chiedere qual è il numero di colonne del tappeto e, per ottenerlo, è necessario capire che è necessario determinare la lunghezza del lato di un quadrato.
Per ottenere un ragionamento più sicuro in merito alla proporzionalità, si può suggerire di porre lo stesso problema con una lunghezza totale maggiore, ad esempio di 1600 cm (o 40 colonne), il che rende il disegno più difficile e può incoraggiare a motivo delle relazioni di lunghezza o numero di colonne (ad esempio, in base al numero di motivi per 80 cm o 160 cm o per 2 colonne o 4 colonne). Vi è quindi uguaglianza nei due numeri di schemi.
Quindi, potremmo suggerire lo stesso problema con 4.840 cm, gli studenti possono quindi utilizzare la proporzionalità per determinare il numero di motivi per 4.800 cm e quindi aggiungere i motivi dalla colonna aggiuntiva.
Questo problema è stato sviluppato in seguito a enormi fallimenti (successo del 13%, incomprensione del 49%) noti per i problemi Pavimentazione (I) (cat 5 & 6) e Pavimentazione (II) (cat 7-9). Il disegno proposto ha indotto fortemente gli alunni ad estenderlo, da una singola colonna o fino al bordo del foglio, senza ricorrere al calcolo.
Sembra che cambiare la variabile non abbia migliorato significativamente i successi.
=== Bibliografia ====
(c) ARMT, 2011-2024