A la pizzeria

Identification

Rallye: 22.II.14 ; catégories: 7, 8, 9, 10 ; domaine: PR
Familles:

• SP - Traiter des suites proportionnelles
• SP/RIP - Effectuer des répartitions proportionnelles

Remarque et suggestion

Résumé

Partager une réduction de prix proportionnellement aux montants des consommations commandées par trois personnes, dans un contexte de facture à la pizzeria.

Enoncé

Tâche de résolution et savoirs mobilisés

- Déterminer le prix des consommations de chacun des trois amis et le total de la note. (André a consommé pour 13,30 €, Bernard pour 15,20 € et Charles pour 17,10 €. Coût total : 45,60 € et en déduire éventuellement que la réduction est de 45,60 – 42 = 3,60 €.) Comprendre qu'une « répartition équitable » de la réduction effectuée sur le coût total doit être faite proportionnellement au coût de la consommation de chacun.

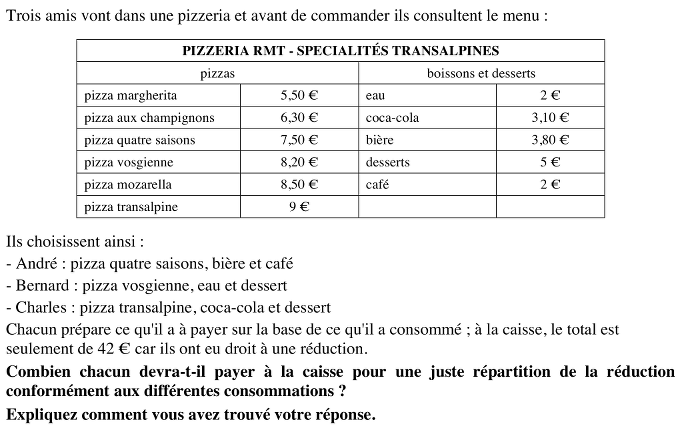
- Pour calculer la somme à payer par chacun, il faut organiser (mentalement ou par un schéma) la correspondance entre les deux grandeurs : prix avant réduction et prix après réductions,

                                A       B     C     tot
  prix avant déduction (en €) 13,30  15,20  17,10 45,60
  prix après réduction (en €)  ?       ?      ?     42

et les valeurs de chacune de ces grandeurs formant quatre couples : (13,3 ; ?) , (15, 2 ; ? ) , (17, 1 ; ? ), (45,60 ; 42), dont seul le dernier est entièrement déterminé.

(Dans le cas où l’on choisirait de calculer les rabais, le couple connu serait (45,60 ; 3,60)

- On entre vraiment dans le problème au moment de déterminer le deuxième terme de chacun des trois premiers couples. La tentation est forte, chez certains élèves, de calculer la différence entre 45,60 et 42, le rabais de 3,60 euros, et de la répartir également entre chacun des trois premiers couples ; chacun obtenant ainsi un rabais de 1,20 euro. Ceux qui savent ou pensent qu’une répartition proportionnelle n’est pas caractérisée par la constances des écarts mais par celle des rapports, calculeront plutôt un rapport entre 45,60 et 42, appelé « rapport ou coefficient de proportionnalité ». Par exemple 42/45,60 = 420/456 = 35/38 ≅ 0.921 qui devra être aussi celui des trois premiers couples de nombres correspondants.

La tâche se poursuit et se termine par l’application du rapport aux trois premiers nombres des trois premiers couples.

Une façon d’obtenir les prix à payer par A, B, C est de multiplier le prix de leurs consommation par le rapport précédent : Prix de A = 13,30 × 35/38 = 12,25 ; B = 15,20 × 35/38 = 14 ; C = 17,10 × 35/38 = 15,75 (en euros).

Il y a de nombreuses algorithmes de résolution à disposition des élèves, selon leurs habitudes : « règle de trois », « proportion », « passage par l’unité », calcul de pourcentages, …

Il est aussi possible de calculer les rabais pour chacun avec un procédé tout à fait analogue.

Notions mathématiques

proportionnalité, addition, soustraction, différence, rapport, nombres décimaux

Résultats

22.II.14

Points attribués sur 1629 copies de 20 sections

Selon les critères déterminés lors de l’analyse a priori :

• 4 points: Réponse correcte (André : 12,25 € ; Bernard : 14 € ; Charles : 15,75 €) avec explications complètes de la procédure
• 3 points: Réponse correcte, mais avec des explications peu claires ou incomplètes
• 2 points: Réponse correcte sans explication
  ou procédure correcte mais réponse erronée due à une erreur de calcul ou pour ne pas avoir donné les valeurs approchées au centième.
• 1 point: Réponse avec des erreurs de calcul mais avec une procédure correcte,
  ou début de procédure correct
• 0 point: Incompréhension du problème

Procédures, obstacles et erreurs relevés

-La réussite à ce problème varie très sensiblement de la catégorie 7 (moyenne de 0,7 point et près de 60% d’incompréhension du problème) à la catégorie 10, où les erreurs sont pourtant encore nombreuses.

- L’obstacle est bien évident et se situe au niveau de la construction du concept de proportionnalité : une majorité des élèves ne « sentent » pas la nécessité d’envisager les rapports des couples correspondants, ils se contentent de conserver les écarts.

- Un premier examen, rapide, des copies de Suisse romande (catégories 7 et 8 seulement) montre que l’erreur « classique » et très majoritaire en catégorie 7 est de répartir le rabais de 3,60 euros en trois rabais de 1,20 euros pour chacun des trois amis, sans se rendre compte que celui qui a consommé le plus devrait avoir un rabais plus important que celui qui a consommé le moins. Il est vrai que, à leur défense, il ne s’agit que de quelques centimes qui ne constituent pas une grande injustice !

En catégorie 8, la confusion est nettement moins fréquente. Les erreurs se situent au niveau des techniques de calcul.

Exploitations didactiques

Les potentialités de ce problème concernent le conflit entre une perception « additive » et une perception « multiplicative » de la situation. Un affrontement est inévitable entre les tenants de l’une ou l’autre des solutions qui apparaîtront vraisemblablement en catégories 7 et 8. C’est une discussion conduite par l’enseignant qui pourra le faire fructifier.

1. procédure « multiplicative » avec facteur 35/38 ( 0,92...) pour passer de la première à la deuxième ligne :

  prix avant déduction (en €) 13,30 15,20 17,10 45,60
  prix après réduction (en €) 12,25 14    15,75 42
  ( rabais (en €               1,05  1,20  1,35 3,60  )

2. procédure « additive » avec répartition du rabais de 3, 60 en 1,20 + 1,20 + 1,20

  prix avant déduction (en €) 13,30 15,20 17,10 45,60
  rabais (en €)               1,20   1,20  1,20  3,60
  prix après réduction (en €) 12,10 14    15,90 42

(Voir aussi les nombreux problèmes de cette famille de tâche)

(c) ARMT, 2014-2024