
Banque de problèmes du RMT
pr34-fr
 |
Banque de problèmes du RMTpr34-fr |
|
Trouver les couples de multiples de 7, proportionnels à 1 et 2, dont la somme est comprise entre 100 et 200; dans un contexte de biscuits partagée entre deux chats.

- Comprendre que les quantités de biscuits mangés par les chats augmentent de jour en jour, que si on en donne trop ça ne suffira pas pour une semaine, que si on en donne trop peu, il y en aura pour plus d’une semaine et qu’il faudra trouver une « ration » qui convient à ces deux contraintes.
- Se rendre compte qu’il faut partir du nombre de biscuits donnés à Thomas et faire plusieurs essais : par exemple, en commençant par 1 biscuit par jour pour Thomas, il en faudra 2 pour Duchesse, continuer pour deux jours, trois jours ou directement pour une semaine et trouver 7 pour Thomas, 14 pour Duchesse et 21 en tout. Voir qu’en deux semaines on arriverait à 14, 28 et 42 en tout. Les 100 biscuits seraient suffisants, contrairement à ce que dit l’énoncé. Répéter ainsi des essais par additions successives, multiplications par 7 … pour déterminer une ou plusieurs possibilités qui conviennent. Par exemple avec 3 biscuits par jour pour Thomas on arrive à une consommation de 63 biscuits en une semaine et on dépasse 100 en deux semaines (126).
Ou bien, organiser les essais pour être sûr de trouver toutes les possibilités. Par exemple en les disposant en lignes ou par des tableaux du genre :
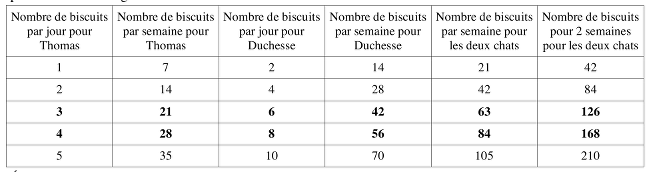
Éliminer les deux premières lignes, car il y aurait assez de biscuits pour 2 semaines, et la dernière car 100 biscuits suffisent pour une semaine.
Et conclure qu’il y a deux possibilités : ou Thomas mange 21 biscuits par semaine et Duchesse 42 ou Thomas mange 28 biscuits par semaine et Duchesse 56.
Ou bien, pour les élèves qui maîtrisent déjà bien le concept de multiples : se rendre compte que le nombre de biscuits mangés chaque jour par les deux chats doit être un multiple de 3.
- En déduire que le nombre de biscuits mangés par les deux chats en une semaine est un multiple de 7 et de 3 (donc de 21) inférieur à 100: 21, 42, 63, 84.
- Écarter 21 et 42 parce que leur double est inférieur à 100, les 100 biscuits seraient alors suffisants pour deux semaines. Conclure que le nombre de biscuits mangés par les deux chats en une semaine est 63 ou 84.
- Comprendre que, comme chaque jour de la semaine, Duchesse mange le double de biscuits de ce que mange Thomas, ce dernier mange le tiers des biscuits donnés aux deux chats.
- En déduire que si les deux chats mangent 63 biscuits en une semaine, alors Thomas en mange 63 : 3 = 21 et Duchesse en mange 42. Alors que si les deux chats mangent 84 biscuits en une semaine, alors Thomas en mange 84 : 3 = 28 et Duchesse 56.
Ou : diviser 63 et 84 par 7 et trouver la quantité journalière de biscuits mangés par les deux chats : 9 et 12. Comme Duchesse mange le double de biscuits de ce que mange Thomas, en déduire que dans le premier cas, Thomas mange chaque jour 3 biscuits et Duchesse 6, et dans le second cas, Thomas mange chaque jour 4 biscuits et Duchesse 8.
En multipliant par 7, on trouve la quantité de biscuits mangés par les deux chats en une semaine (21 Thomas et 42 Duchesse dans le premier cas et 28 Thomas et 56 Duchesse dans le second cas).
double, triple, multiple, proportionnalité
Points attribués sur 997 classes de 17 sections:
| Catégorie | 0 | 1 | 2 | 3 | 4 | Nb. de classes | Moyenne |
|---|---|---|---|---|---|---|---|
| Cat 3 | 298 (64%) | 72 (15%) | 75 (16%) | 7 (2%) | 14 (3%) | 466 | 0.64 |
| Cat 4 | 263 (50%) | 98 (18%) | 130 (24%) | 19 (4%) | 21 (4%) | 531 | 0.94 |
| Total | 561 (56%) | 170 (17%) | 205 (21%) | 26 (3%) | 35 (4%) | 997 | 0.8 |
| Rappel: Le problème est résolu dans les conditions particulières du RMT: classe entière, élèves en autonomie complète, 5 à 7 problèmes à résoudre, une seule feuille de réponses par problème. | |||||||
(c) ARMT, 2011-2024