La course des monstres
Identification
Rallye:
25.F.17 ; catégories:
8, 9, 10 ; domaines:
PR,
GPFamilles:
Envoyer une remarque ou une suggestion
Résumé
Parmi des concurrents se déplaçant dans un labyrinthe organisé sur un quadrillage et partant de positions différentes en direction d’un même but, trouver le gagnant à partir d’informations relatives à des rapports de vitesses entre les concurrents.
Enoncé
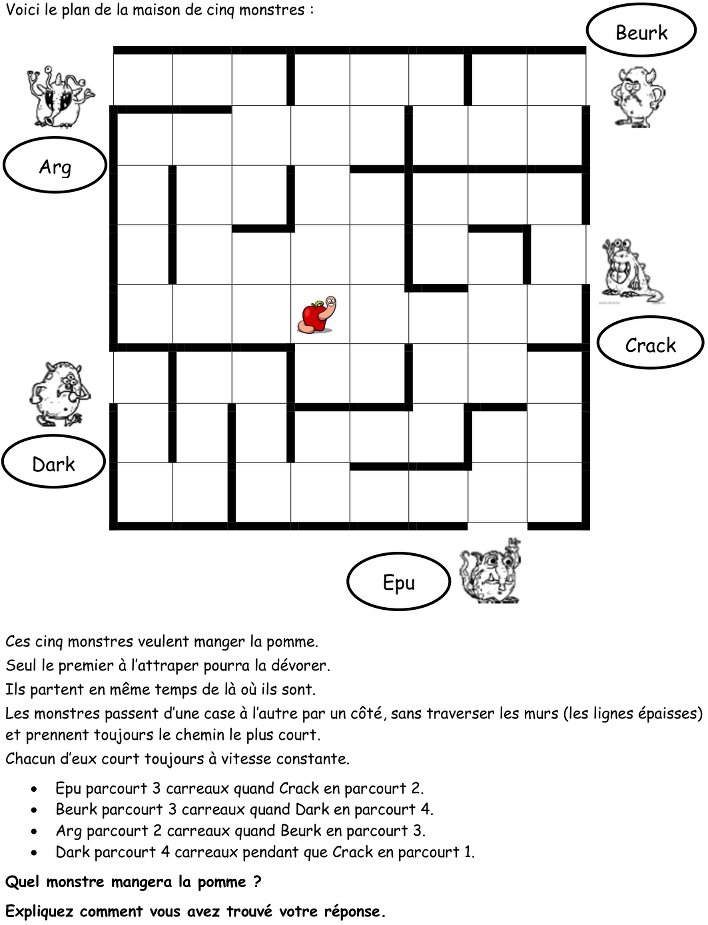
Tâche de résolution et savoirs mobilisés
Analyse a priori
Les conditions liées à la vitesse de chaque monstre sont numérotées de 1 à 4.
- Comprendre que les distances ont pour unité de mesure une case du quadrillage.
- Remarquer que les distances à parcourir par les monstres pour atteindre la pomme sont différentes.
- Comprendre qu’il faut tenir compte à la fois de la vitesse et de la distance pour résoudre ce problème : Ce n’est pas forcément ni le plus rapide ni le plus proche qui attrape la pomme.
- Repérer le chemin le plus court pour chaque monstre et relever la distance à parcourir en nombre de carreaux :
- Comparer les parcours des monstres 2 à 2 dans le labyrinthe en s’appuyant sur chaque condition :
- soit en utilisant un raisonnement numérique. Par exemple, en utilisant la condition 2 il faut plus de 3 bonds et moins de 4 bonds de 3 carreaux à Beurk pour atteindre la pomme, alors qu’il faut plus de 4 bonds de 4 carreaux à Dark. Beurk arrivera donc avant Dark ;
- soit en déplaçant des pions sur les parcours. Par exemple, à chaque fois qu’on avance le pion sur le parcours de Beurk de 3 carreaux, on avance le pion sur le parcours de Dark de 4 carreaux. Constater que le pion de Beurk atteint ou dépasse la pomme avant celui de Dark.
On trouve :
- D’après la condition 2, Beurk arrive avant Dark.
- D’après la condition 4, Dark arrive avant Crack, donc d’après la première déduction faite Beurk arrive avant Crack.
- D’après la condition 1, on constate qu’Epu et Crack arrivent en même temps donc Beurk arrive avant Epu.
- D’après la condition 3, Beurk arrive avant Arg : un moment dans leur parcours ils se retrouvent tous les deux sur le même carreau ; à ce moment il reste 2 carreaux à chacun pour arriver à la pomme mais comme Beurk court plus vite que Arg (d’après la condition 3) alors Beurk arrive avant lui.
Finalement Beurk arrive avant tous les autres monstres. C’est lui qui mangera la pomme.
Notions mathématiques
vitesse, rapport
Résultats
25.F.17
Points attribués, sur 96 classes de 16 sections:
| Catégorie | 0 | 1 | 2 | 3 | 4 | Nb. de classes | Moyenne |
|---|
| Cat 8 | 5 (9%) | 5 (9%) | 16 (29%) | 15 (27%) | 15 (27%) | 56 | 2.54 |
|---|
| Cat 9 | 1 (4%) | 7 (30%) | 4 (17%) | 3 (13%) | 8 (35%) | 23 | 2.43 |
|---|
| Cat 10 | 1 (6%) | 1 (6%) | 3 (18%) | 1 (6%) | 11 (65%) | 17 | 3.18 |
|---|
| Total | 7 (7%) | 13 (14%) | 23 (24%) | 19 (20%) | 34 (35%) | 96 | 2.63 |
|---|
| Rappel: Le problème est résolu dans les conditions particulières du RMT: classe entière, élèves en autonomie complète, 5 à 7 problèmes à résoudre, une seule feuille de réponses par problème. |
Selon les critères déterminés lors de l’analyse a priori :
- 4 points: Réponse correcte (Beurk) avec une explication claire et complète de la procédure (description de la procédure et des déductions faites qui permettent de conclure)
- 3 points: Réponse correcte (Beurk) avec une explication incomplète (absence d’une ou deux déductions)
- 2 points: Réponse correcte sans explications
ou réponse incorrecte, mais avec une procédure cohérente (par exemple prise en compte des distances et des vitesses mais non prise en compte du chemin le plus court pour au moins l’un des monstres ou erreur sur la longueur d’un parcours ou erreurs de calcul) - 1 point: Début de recherche (repérage des distances les plus courtes pour chaque monstre ou début de rangement des monstres selon leur vitesse)
- 0 point: Incompréhension du problème



