
Banque de problèmes du RMT
pr48-fr
 |
Banque de problèmes du RMTpr48-fr |
|
Envoyer une remarque ou une suggestion
Répartir 84 objets en trois parties dont la deuxième vaut le double de la première et la troisième le double de la deuxième

Une première procédure, par essais et vérification demande de savoir « calculer le double d’un nombre naturel choisi comme premier essai » deux fois de suite, puis « d’additionner les trois nombres » et de « comparer cette somme à 84 » pour décider si elle est correcte ou s’il est nécessaire de poursuivre les essais. On arrive ainsi à la solution 12 ; 24 ; 48 dont la somme est 84. Le nombre d’essais dépend du premier choix qui peut être pris au hasard ou déjà « estimé » vraisemblable, puis de l’organisation des essais suivants qui peuvent être aussi pris au hasard ou déduits du précédent, en l’augmentant ou le diminuant selon que la somme est inférieure ou supérieure à 84.
Une deuxième procédure demande une perception généralisée des relations entre les trois nombres et leur somme : pour « n’importe quel choix » du nombre d’oranges d’une des caisses, avec les concepts « d’unité commune » et de « substitution » il est possible d’exprimer la somme (84) des trois nombres cherchés au moyen d’un seul. En partant par exemple du nombre d’oranges de la petite caisse, encore indéterminé, on peut savoir qu’il se retrouvera deux fois (le double) dans celui de la deuxième caisse, puis quatre fois (le double du double) dans la troisième et finalement (par addition) sept fois dans le total des trois caisses. La relation entre sept fois ce nombre, toujours indéterminé, et 84 oranges se traduit par la multiplication lacunaire 7 x … = 84 ou par la division 84 : 7 = 12. Cette deuxième procédure se situe à un niveau cognitif beaucoup plus élevé que la première ; on peut la qualifier de pré-algébrique car elle se construit sur une quantité indéterminée (ou « encore inconnue »). Pour y accéder, l’élève, doit se référer à des représentations mentales ou graphiques. (Procédure rhétorique, qui peut déjà apparaître en cat. 4 car on la trouve en cat. 5 dans Les prunes (25.II.11), plus complexe) Des schémas ou dessins sont une aide souvent efficace pour faire émerger ce type de procédure.
nombre naturel, division, multiplication, addition, décomposition additive, proportionnalité, répartition proportionnelle
Points attribués sur 1519 classes de 18 sections:
| Catégorie | 0 | 1 | 2 | 3 | 4 | Nb. de classes | Moyenne |
|---|---|---|---|---|---|---|---|
| Cat 3 | 198 (29%) | 123 (18%) | 108 (16%) | 141 (21%) | 117 (17%) | 687 | 1.79 |
| Cat 4 | 138 (17%) | 138 (17%) | 164 (20%) | 202 (24%) | 190 (23%) | 832 | 2.2 |
| Total | 336 (22%) | 261 (17%) | 272 (18%) | 343 (23%) | 307 (20%) | 1519 | 2.02 |
| Rappel: Le problème est résolu dans les conditions particulières du RMT: classe entière, élèves en autonomie complète, 5 à 7 problèmes à résoudre, une seule feuille de réponses par problème. | |||||||
- Les feuilles blanches sont très rares, ce qui atteste d’une bonne appropriation de la situation. Même sur les copies correspondant à « l’incompréhension du problème », il y a des caisses dessinées, des tentatives d’addition, des répartitions.
- La procédure par essais est majoritaire parmi les centaines de copies analysées.
Exemple 1
Un tableau de 10 lignes:
5 - 10 - 15 = 30 non
6 - 12 - 18 = 36 non
...
12 - 24 - 48 = 84 oui
Certains de ces tableaux ont 12 lignes et commencent par 1 x 2 = 2 x 2 = 4 x 2 + 1 = 7 suivi de 2 x 2 = 4 x 2 = 8 + 4 + 2 = 14
Exemple 2
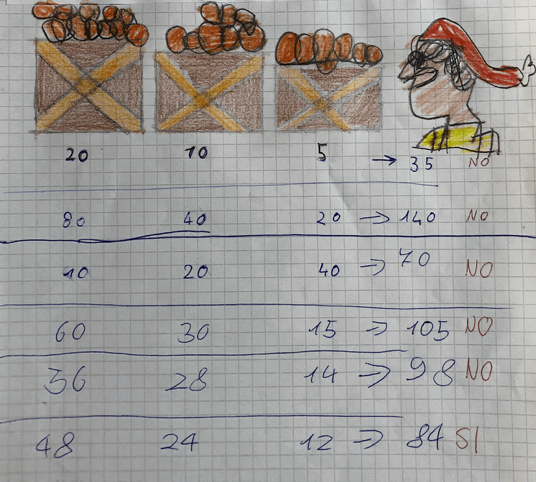
Le premier essai est 20-10-5 (du plus grand au plus petit) qui donne un total de 35 insuffisant (noté “NO”). Les trois essais suivants sont respectivement “quatre fois”, “deux fois” et “trois fois” les nombres du premier avec des totaux de 140, 70 et 105 qui se rapprochent progressivement de 84.
Le cinquième essai semble judicieusement choisi, le nombre 36 est en compris entre 40 et 60 des deuxième et quatrième essais comme 84 est compris entre 70 et 105 de ces deux essais.
Mais en partant de 36, les élèves font une erreur pour la caisse moyenne (28 n’est pas la moitié de 36 ; il aurait fallu écrire 18, puis 9 pour la petite). Cette erreur n’a pas de conséquence sur la suite des essais, mais puisque la somme, erronée, de 98 est plus grande que 84, la logique aurait voulu que l’essai suivant commence par un nombre plus petit que 36. Le choix de 48 semble donc être dû au hasard.
Cette copie montre que les élèves maîtrisent la relation « le double » et son inverse « la moitié », qu’ils organisent les essais de manière à peu près cohérente. Pour en savoir plus sur le niveau réel de construction de ces connaissances, il faudrait pouvoir s’entretenir directement avec eux.
Certaines fois, les explications ne donnent pas le détail des opérations mais parlent toutefois d'un grand nombre d'essais qui ont vraisemblablement été faits.
Exemple 3
Réponse 48, 24, 12
Per trovare la nostra risposta abbiamo fatto tanti tentativi e poi abbiamo scritto un numero abbastanza grande che abbiamo diviso in due e veniva il numero della cassetta media. Abbiamo ripetuto questo procedimento sul numero della cassetta media e veniva il numero della cassetta piccola
Pour trouver notre réponse nous avons fait de nombreuses essais puis nous avons écrit un nombre suffisamment grand que nous avons divisé en deux et le numéro de la caisse moyenne est sorti. Nous avons répété ce processus sur le numéro de la caisse moyenne et le numéro de petite caisse est sorti
- Les procédures par division par 7 sont plus rares et apparaissent plus souvent en catégories 4 qu'en catégorie 3. Elles s'appuient sur des représentations de segments ou de carrés.
Exemple 4

La majorité des réponses erronées 14; 28; 84 vient de la dicision de 84 par 3 pour obtenir le nombre d'oranges de la caisse moyenne, sns vérifier la somme.
Faire expliquer à quelques groupes leur procédure.
On peut être certain que les premiers échanges feront apparaître clairement la procédure par essais et les différentes manières de les organiser.
On peut espérer, comme l’ont montré nos premières analyses a posteriori que certains groupes auront procédé au niveau d’une compréhension plus généralisée en référence à une quantité encore indéterminée d’oranges dans une des caisses, qui deviendra une unité commune. Si cette seconde procédure n’apparaît pas encore dans le débat collectif, il faut admettre que les élèves n’ont pas encore atteint le niveau nécessaire de maturité et que, par conséquent, il ne serait pas judicieux de « l’enseigner » (selon la conception socio-constructiviste du RMT). Si elle apparaît, il est alors important que les élèves qui l’ont utilisée l’expliquent aux autres, dans leur langage.
Institutionnalisation
- Les différentes manières d’organiser les essais pour être certain qu’il n’y a qu’une solution : 12 ; 24 ; 48.
- Les règles élémentaires de l’organisation : par exemple si l’on choisit 7 oranges dans la petite caisse, le total sera 7 + 14 + 28 = 49 qui est plus petit que 84, par conséquent les essais successifs pour la petite caisse doivent être plus grands que 7.
- En cas d’apparition de la seconde procédure, insister sur une représentation graphique des quantités permettant de décrire les contenus des trois caisses et le total selon l’unité commune de la petite caisse : 1 ; 2 ; 4 ; 7. (Ces quatre nombres sont les caractéristiques de cette situation particulière des caisses d’oranges et vont préfigurer la notion de « proportionnalité »)
Structuration (construction)
Les phases précédentes, de résolution par groupes, de débat collectif et d’institutionnalisation occupent la classe durant une ou deux périodes de travail, au cours desquelles certains élèves seront actifs et d’autres (une majorité ?) se contenteront d’enregistrer des fragments de connaissances. Il faut maintenant consolider et renforcer ces connaissances pour certains, les découvrir ou redécouvrir pour d’autres. Il faut se mettre au travail et « étudier ».
- Chacun (dans son cahier par exemple) doit noter des traces précises de l’activité : une liste organisée des essais. Si l’on veut que cette liste soit considérée comme utile, aux yeux de l’élève, pour la résolution du problème particulier des caisses d’oranges, elle devrait être complète (exhaustive). Par exemple en quatre colonnes : nombres d’oranges de la petite, de la moyenne, de la grande et du total ; faisant apparaître la suite des nombres naturels, des multiples de 2, de 4 et de 7. (l’activité est certes « répétitive », mais nécessaire car les quatre ensembles de nombres le sont aussi !)
Cette liste est apparue spontanément dans quelques copies d’élèves lors de l’épreuve, elle n’était pas obligatoire mais répondait peut-être à la demande Montrez comment vous êtes arrivés à votre réponse.
- Chacun devrait aussi dessiner une représentation graphique de la situation ; par des dessins figuratifs comme l’ont fait de nombreux groupes lors de l’épreuve, mais aussi par des dessins « opératoire » (segments, carrés, cercles) qui permettent compter les unités communes.
La vérification des connaissances par la résolution d’un ou deux autre(s) problème de la Banque sur le même thème des partages proportionnels où sont indiqués ici : Titre, (rallye et catégorie), Résumé, Relations (algébriques) entre les grandeurs en jeu, Moyennes des point obtenus par catégorie.
Une photo d'Afrique (19.I.03 ; 3-4) Trouver deux nombres naturels tels que l'un est le double de l'autre et dont la somme est 36, dans un contexte d’animaux de deux espèces. a + b = 36 ; b = 2a - cat 3 / 4 : 2,4 / 2,9
Les châtaignes de Charles (I)22.II.01 ; 3-4) Calculer la somme des quatre nombres : 18, 18, la moitié de 18 et le double de 18 ; dans un contexte de récolte de châtaignes b = 2a ; c = 2b ; b = 18 ; (a + b + c + d) – (a + b + c) = 18 . - cat 3 / 4 : 2,5 / 3.1
Les autocollants (21.F.03 ; 3-4) Décomposer 90 en une somme de trois termes proportionnels à 1, 3 et 5, dans un contexte d’autocollants à répartir sur trois endroits. a + b + c = 90 ; b = 3a ; c = 5a - cat 3 / 4 : 2,3 / 2,9
Drôle de pizza (12.II.09 ; 5-6) Décomposer une pizza rectangulaire de 4 m (!) en quatre parties de longueurs C, J, O et F telles que : J est le double de C et la moitié de O, F est le quart de la partie la plus longue. a + b + c + d = 4 ; a = b/2 ; c = 2b ; d = c/4 (pas de résultats)
Toujours le double (21.II.04 ; 3-5) Chercher à décomposer 100, ou sinon le plus grand nombre naturel inférieur à 100, en trois nombres proportionnellement à 1, 2 et 4; dans un contexte de billes à répartit dans trois boîtes. a + b + c < 100 ; b = 2a ; c = 2b - cat 3 / 4 / 5 : 1,4 / 2,0 / 2,5
Les châtaignes de Charles (II) (22.II.09 ; 5-7) Décomposer 81 en une somme de quatre nombres proportionnellement à 1, 2, 4 et 2, dans un contexte de récolte de châtaignes. a + b + c + d = 81 ; b = 2a ; c = 2b ; d = c/2 - cat 5 / 6 / 7 : 2,0 / 2,0 / 2.5
On peut espérer que, après cette exploitation du problème Oranges, les élèves conserveront une mémoire d’une situation de répartition proportionnelle (même si le mot « proportionnelle » n’est pas utilisé car nettement prématuré), l’idée d’une organisation d’essais ou d’une unité commune, ainsi qu’une sensibilisation aux ensembles de multiples (de 2, 4 et 7) ! Tout ceci au cours d’une semaine de travail en mathématiques.