
Banque de problèmes du RMT
pr56-fr
 |
Banque de problèmes du RMTpr56-fr |
|
Envoyer une remarque ou une suggestion
Trouver l’aire d’un rectangle décomposé en 9 rectangles (grille de 3 × 3) dont on connaît l’aire de cinq d’entre eux.
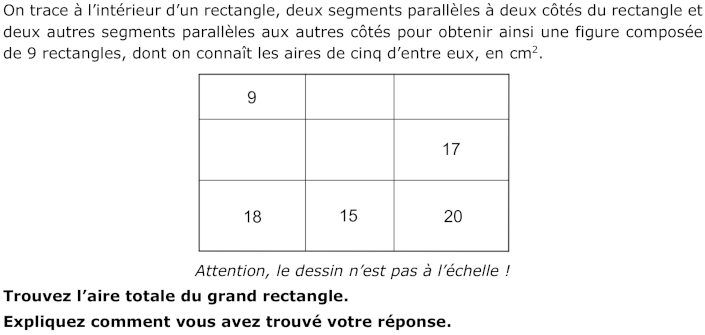
- Se rendre compte que les neuf rectangles s’organisent en 3 « colonnes » de rectangles avec leur dimension « horizontale » commune et 3 « lignes » de rectangle avec leur dimension « verticale » commune.
- La résolution du problème nécessite la connaissance que l’aire d’un rectangle est proportionnelle à chacune de ses deux dimensions.
- À partir de cette connaissance une série de déductions permet de calculer progressivement (mentalement pour certaines) les aires des quatre rectangles encore inconnus. Par exemple 9 et 18 définissent le rapport de proportionnalité (2) des aires de la première et de la troisième ligne et aboutit aux aires 7,5 et 10 respectivement pour le deuxième et le troisième rectangle de la première ligne ; 10 et 17 définissent le rapport de proportionnalité (1,7) /des aires de la première et de la deuxième ligne et aboutit aux aires 9 x 1,7 = 15,3 et 7,5 x 1,7 = 12,75 respectivement pour le premier et le deuxième rectangle de la deuxième ligne.
- L’aire totale du rectangle est (9 + 7,5 + 10) + (15,3 + 12,75 + 17) + (18 + 15 + 20) = 124,55
- Pour ceux qui ne maîtrisent pas la connaissance mentionnée précédemment, il y a des moyens de l’utiliser implicitement en donnant des dimensions fictives aux rectangles, à partir de leurs aires : par exemple on peut imaginer des dimensions, comme 6 x 3 pour le rectangle d’aire 18, déterminer mentalement que son voisin de droite sera de dimensions 5 x 3, le suivant 20/3 x 3 etc. (Cette méthode est correcte pour la détermination des aires, en étant conscient que d’un choix à l’autre des dimensions fictives, les rectangles ne sont pas semblables car il y a une infinité de rectangles du plus « allongé » possible au carré !)
rectangle, aire, rapport, proportionnalité.
Résultats sur 1225 classes de 20 sections:
| Catégorie | 0 | 1 | 2 | 3 | 4 | Nb. de classes | Moyenne |
|---|---|---|---|---|---|---|---|
| Cat 8 | 355 (43%) | 104 (12%) | 43 (5%) | 148 (18%) | 184 (22%) | 834 | 1.64 |
| Cat 9 | 72 (35%) | 13 (6%) | 8 (4%) | 23 (11%) | 92 (44%) | 208 | 2.24 |
| Cat 10 | 54 (30%) | 14 (8%) | 4 (2%) | 24 (13%) | 87 (48%) | 183 | 2.42 |
| Total | 481 (39%) | 131 (11%) | 55 (4%) | 195 (16%) | 363 (30%) | 1225 | 1.86 |
| Rappel: Le problème est résolu dans les conditions particulières du RMT: classe entière, élèves en autonomie complète, 5 à 7 problèmes à résoudre, une seule feuille de réponses par problème. | |||||||
Les analyses a posteriori des sections de RV et de SI permettent de constater que l'obstacle important est la non perception de la proportionnalité entre les aires des rectangles, d'une ligne à l'autre ou d'une colonne à l'autre. Obstacle rencontré en particulier par 55 % des groupes d'élèves de catégorie 8.
La réponse la plus fréquente est 15, 12 et 17 pour la ligne centrale et moins fréquemment, 9, 6 et 11 pour la première ligne.
Les commentaires ou explications sont tous les mêmes, à quelques variation près: dans la troisième ligne, la différence entre 18 et 15 est 3 et la différence entre 15 et 20 est 5; pour la deuxième line nous avons calculé 17 - 5 = 12, puis 12 + 3 = 15; pour la première ligne on part de 9, on enlève 3 pour arriver à 6 et on ajoute 5 pour trouver 11.
Certains groupes remarquent que, dans la première colonne 9 est la moitié de 18 et calculent alors la moitié de 15 et la moitié de 20 pour les deux autres aires de la première ligne: 7,5 et 10. On pourrait croire qu'ils ont perçu la proportionnalité mais il n'en est rien. Ils retrouvent la procédure additive pour la seconde ligne, avec les réponses 15, 12 et 17. (23% des copies de la section de RV).
Pour les autres copies (45%) de catégorie 8, la réponse correcte est trouvée, soit par proportionnalité avec le facteur 1/2 entre la troisième ligne et la première et le facteur 1,7 entre la première et la deuxième; soit en choisissant des dimensions pour la largeur des rectangles de la troisième ligne. Dans le cas du choix de 5 cm pour la largeur de cette ligne, les calculs se déroulent sans difficulté, les trois "longueurs" des rectangles sont, de droite à gauche, respectivement 4, 3 et 3,6. Dans le cas du choix de 3 cm, ces les deux premières "longueurs" sont 6 et 5 mais la troisième est une approximation de 6,67 au lieu de 20/3 et des reports approximatifs sur les autres qui, fréquemment n'aboutissent qu'à une approximation non explicite de la réponse finale 124,55.
Si l'on observe la troisième et la première lignes de rectangles, les nombres 18, 15 20 correspondent à 9 et deux nombres encore à déterminer par calcul mental élémentaire: 7,5 et 10. Les savoirs nécessaires se limitent à la relation entre les mesures des côtés d'un rectangle dont le produit donne son aire: la formule A = b x c. Puisque l'aire du premier rectangle de la première ligne (9, en cm$^2$) est la moitié de celle du premier rectangle de la troisième ligne (18) et que ces deux rectangles sont de de même longueur, on peut en déduire que la largeur du rectangle de la première ligne est la moitié de celle de celui de la troisième ligne, que les largeurs des deux autres rectangles de la première ligne sont aussi la moitié de celles des deux suivants de la troisième ligne, que par conséquent ce rapport (de proportionnalité) 1/2 sera aussi celui des aires des rectangles correspondants.
Une question qu'on doit se poser est de savoir pourquoi de très nombreux élèves de catégorie 8 (et suivantes, ainsi que plusieurs membres du "Groupe proportionnalité" en première analyse) ne ne perçoivent pas le rapport des aires d'une ligne à l'autre ou d'une colonne à l'autre. (Ceux qui en sont encore restés à une perception additive (15, 12 et 17 pour la ligne centrale) ou ceux qui doivent passer par un cas particulier en choisissant des mesures de côtés pour un premier rectangle (par exemple 2 x 9 = 18 --> 1 x 9 = 9 ; 2 x 7,5 = 15 --> 1 x 7,5 = 7,5 ; 2 x 10 =20 --> 1 x 10 = 10).
Il y a de nombreuses réponses différentes à cette question, dont dépend l'exploitation didactique de cette ignorance illustrée par l'analyse statistique des résultats ci-dessus de 1225 copies.
Si l'on considère que cette ignorance ou insuffisance des savoirs concernant la formule de l'aire du rectangle et/ou de la proportionnalité entre une dimension (l'autre étant constante) et l'aire d'un rectangle est une fatalité,
- si l'on pense que cette insuffisance est due aux programmes officiels, aux manuels ou aux enseignants,
- si l'on pense que le problème est trop difficile pour les élèves à qui on l'a proposé,
on se contentera de "bien expliquer" la démarche à suivre à la majorité d'élèves en échec et à constater un peu plus tard que la situation ne s'est pas améliorée.
A ce propos, les mêmes observations, se retrouvent dans l'analyse des résultats des problèmes Le terrain du père François (11.II.16), Le potager (I) (26.II.12), Le potager (II) (26.II.15) où, au lieu de rectangles dont une dimension est constante, il s'agit de triangles de même "hauteur" dont la proportionnalité entre la mesure de la "base" et celle de l'aire n'est pas perçue.
La rubrique suivante propose quelques activités pour découvrir la richesse de cette situation où l'on ne connaît que les mesures des aires de 5 des 9 rectangles.
Exemples d'activités en vue d'un parcours didactique avec la classe
À expérimenter en classe, selon des modalités déterminées par l'enseignant; avec envoi de description et commentaires pour rendre compte de l'opportunité de l'activité pour la construction des savoirs (notés en italique).
Une des hypothèses pour expliquer l'obstacle que rencontrent les élèves - et même de nombreux enseignants - dans la perception des rapports de proportionnalité entre les aires et les mesures de longueurs des rectangles est liée à l'absence de données sur les mesures de longueurs (dimension 1D) dans la figure. Les cinq nombres donnés sont des mesures d'aires (dimension 2D) et une réflexion préalable est nécessaire pour constater que ces cinq mesures ne précisent pas le rapport entre les deux dimensions de chaque rectangle.
a) Revenir à la figure en la faisant dessiner par chaque élève, sur papier quadrillé pour faciliter la construction, en choisissant le carreau du quadrillage comme unité d'aire. (En commençant par exemple par la droite horizontale inférieure sur laquelle sont alignés les trois rectangles d'aires 18, 15 et 20 et la droite verticale de gauche sur laquelle sont alignés les trois rectangles de la première colonne d'aires 18, ? et 9. (Cette activité de dessin se fait collectivement, avec de nombreuses interactions, sous la conduite de l'enseignant.)
Premier savoir élémentaire : ces deux droites sont perpendiculaires. Deuxième savoir (au moment où il faut esquisser un troisième côté, horizontal, du rectangle inférieur gauche): Il y a plusieurs rectangles d'aire 18, une infinité même ! - ou - on peut choisir n'importe quel nombre pour exprimer la dimension verticale de ce rectangle (largeur ou longueur).
Si l'on choisit par exemple 3 comme distance entre les deux premières droites horizontales (en côté de carré du quadrillage) ou mesure verticale du côté du premier rectangle, l'autre dimension, horizontale est déterminée : 6, car 3 x 6 = 18.
Rappel des notions de distance entre deux droites parallèles, de mesures de longueur (1D): 3 et 6, de mesures d'aires (2D) : 18, de la formule de l'aire du rectangle et des deux types d'unités qu'elle fait intervenir, ...
Les dimensions de trois autres rectangles sont ainsi définies : 9 = 1,5 x 6 ; 15 = 3 x 5 et 20 = 3 x 20/3.
les aires des deux autres rectangles de la première ligne: 7,5 et 10 peuvent se calculer à partir des dimensions découvertes précédemment ou par proportionnalité: les aires des rectangles du bas sont proportionnelles à celles des rectangles du haut, de rapport 9/18 = 1/2 ou 18/9 = 2.
Pour la ligne centrale, les procédures sont les mêmes. Selon le premier choix de 3 comme distance entre les deux premières droites horizontales (en côté de carré du quadrillage), on trouve sa dimension verticale à partir de l'aire donnée de son troisième rectangle, 17, et de la longueur du troisième rectangle de la troisième ligne, 20/3 qui permettent d'obtenir 17/(20/3) = 17 x (3/20) = 51/20 = 2,55
Aux savoirs du domaine de la géométrie, s'ajoutent ceux de l'arithmétique: rapport de deux nombres naturels, nombre rationnel sous forme décimale ou de fraction pour ceux qui ne sont pas décimaux, simplification des fractions, multiplication de fractions, nombres ou fractions inverses, proportionnalité, ...
b) Comparaison des figures des neuf rectangles selon des choix différents d'une première dimension. (Chaque élève fait un autre choix d'une première dimension, d'un des cinq rectangles ; une comparaison doit faire apparaître des rapports différents des dimensions des rectangles (certains plus "allongés" que d'autres) mais toujours avec les mêmes aires dont la somme est aussi toujours la même : (9 + 7,5 + 10) + (15,3 + 12,75 + 17) + (18 + 15 + 20) = 124,55 (en carreaux du quadrillage)
Savoirs: rectangles de mêmes aires mais non semblables (similitude), conservation des rapports de proportionnalité entre aires des rectangles d'une ligne à l'autre ou d'une colonne à l'autre
c) Questions ou développements (exemples)
- Le rapport entre les aires des rectangles de la première ligne et celles des rectangles de la troisième ligne est 2. Celui entre les aires des rectangles la première ligne et celles des rectangles de la deuxième ligne est 1,7. Ces deux rapports permettent-ils de calculer le rapport entre les aires des rectangles de la deuxième ligne et celles des rectangles de la troisième ligne ?
- Si l'on ajoutait une quatrième colonne de trois rectangles à la figure des neuf rectangles, au lien des cinq aires données, combien faudrait-il en donner au minimum pour pouvoir trouver l'aire totale.
- L'un des neuf rectangles pourrait-il être carré ?
- ...
d) autres problèmes de rectangles juxtaposés qui font appel aux dimensions de ces figures et de leurs aires: La table de jardin (15.I.12), La boîte (11.F.09), Le parquet (23.I.14)