
Banca di problemi del RMT
pr56-it
 |
Banca di problemi del RMTpr56-it |
|
Envoyer une remarque ou une suggestion
Trovare l’area di un rettangolo scomposto in 9 parti rettangolari (griglia 3 × 3) conoscendo l’area di cinque di essi.
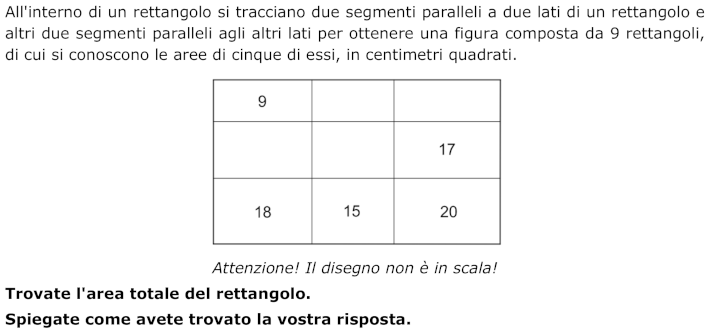
- Rendersi conto che i nove rettangoli si organizzano in tre “colonne” di rettangoli aventi il lato orizzontale della stessa misura e in tre “righe” di rettangoli aventi il lato verticale della stessa misura.
- La risoluzione del problema necessita della conoscenza che l’area di un rettangolo è proporzionale alle misure di ciascuno dei suoi lati.
- A partire da questa conoscenza, una serie di deduzioni permette di calcolare progressivamente (mentalmente per alcuni) le aree dei quattro triangoli ancora incogniti. Per esempio, 18 e 9 definiscono il rapporto di proporzionalità (2) fra le aree della terza e della prima riga e determinano le aree 7,5 e 10 rispettivamente per il secondo e per il terzo rettangolo della prima riga. Analogamente 17 e 10 definiscono il rapporto di proporzionalità (1,7) fra le aree della seconda e della prima riga e determinano le aree 9 × 1,7 = 15,3 e 7,5 × 1,7 = 12,75 rispettivamente per il primo e per il secondo rettangolo della seconda riga.
- L’area totale del rettangolo è dunque: (9 + 7,5 + 10) + (15,3 + 12,75 + 17) + (18 + 15 + 20) = 124,55.
- Per chi non padroneggia la conoscenza menzionata, ci sono modi di utilizzarla implicitamente attribuendo dei valori arbitrari ai lati dei rettangoli, a partire dalle loro aree: per esempio si possono immaginare le dimensioni 6 3 per il rettangolo di area 18, determinare mentalmente che il rettangolo a fianco avrà dimensioni 5 3, il seguente 20/3 3 , ... (Questo metodo è corretto per la determinazione delle aree, con la consapevolezza che, con diverse scelte delle dimensioni arbitrarie, i rettangoli variano la loro forma in una infinità di modi, da quello più “allungato” possibile, al quadrato!).
rettangolo, area, rapporto, proportionnalità.
Résultats sur 1225 classes de 20 sections:
| Categoria | 0 | 1 | 2 | 3 | 4 | Nb.classi | Media |
|---|---|---|---|---|---|---|---|
| Cat 8 | 355 (43%) | 104 (12%) | 43 (5%) | 148 (18%) | 184 (22%) | 834 | 1.64 |
| Cat 9 | 72 (35%) | 13 (6%) | 8 (4%) | 23 (11%) | 92 (44%) | 208 | 2.24 |
| Cat 10 | 54 (30%) | 14 (8%) | 4 (2%) | 24 (13%) | 87 (48%) | 183 | 2.42 |
| Totale | 481 (39%) | 131 (11%) | 55 (4%) | 195 (16%) | 363 (30%) | 1225 | 1.86 |
| Si ricorda che il problema è stato affrontato nelle condizioni particolari del RMT: intera classe, allievi in completa autonomia, da 5 a 7 problemi da risolvere, un solo foglio risposta per problema. | |||||||
Le analisi a posteriori delle sezioni RV e SI permettono di constatare che il principale ostacolo riguarda la non percezione della proporzionalità tra le aree dei rettangoli, da una riga all'altra o da una colonna all'altra. Ostacolo riscontrato dal 55% dei gruppi di allievi della categoria 8, in particolare.
Le risposte più comuni sono 15, 12 e 17 per la riga centrale e, meno frequentemente, 9, 6 e 11 per la prima riga. Le spiegazioni sono tutte simili, con qualche variante: nella terza riga, la differenza tra 18 e 15 è 3 e la differenza tra 15 e 20 è 5; per la seconda riga, abbiamo calcolato 17 - 5 = 12, quindi 12 + 3 = 15; per la prima riga, partiamo da 9, sottraiamo 3 per arrivare a 6 e aggiungiamo 5 per trovare 11.
Alcuni gruppi notano che, nella prima colonna, 9 è la metà di 18 e poi calcolano metà di 15 e metà di 20 per le altre due aree della prima riga: 7,5 e 10. Si potrebbe pensare di aver afferrato la proporzionalità, ma non è così. Gli allievi ritrovano la procedura additiva per la seconda riga, con le risposte 15, 12 e 17 (il 23% degli elaborati della sezione RV).
Per gli altri elaborati (45%) della categoria 8, la risposta corretta si trova o per proporzionalità con il fattore 1/2 tra la terza riga e la prima e il fattore 1,7 tra la prima e la seconda; oppure scegliendo le dimensioni per la larghezza dei rettangoli della terza riga. Nel caso della scelta di 5 cm per la larghezza di questa riga, i calcoli procedono senza difficoltà, le tre "lunghezze" dei rettangoli sono, da destra a sinistra, rispettivamente 4,3 e 3,6. Nel caso della scelta di 3 cm, queste prime due "lunghezze" sono 6 e 5 ma la terza è un'approssimazione di 6,67 invece di 20/3 e rapporti approssimativi sulle altre che, frequentemente, si traducono solo in un'approssimazione non esplicita della risposta finale 124,55.
Una domanda che ci si deve porre è perché così tanti allievi della categoria 8 (e successive, così come diversi membri del "Gruppo Proporzionalità" nell'analisi iniziale) non percepiscono il rapporto tra le aree di una riga e l'altra o di una colonna e l'altra (coloro che sono ancora bloccati con la percezione additiva (15, 12 e 17 per la linea centrale) o coloro che devono affrontare un caso speciale scegliendo le misure dei lati per un primo rettangolo (ad esempio, 2 x 9 = 18 --> 1 x 9 = 9; 2 x 7,5 = 15 --> 1 x 7,5 = 7,5; 2 x 10 = 20 --> 1 x 10 = 10)
Ci sono molte risposte diverse a questa domanda, da cui dipende l’utilizzazione didattica di questa “non percezione” illustrata dall'analisi statistica dei risultati riportati più sopra di 1.225 elaborati.
Se consideriamo inevitabile questa conoscenza insufficiente riguardante la formula dell'area del rettangolo e/o della proporzionalità tra una dimensione (l'altra essendo costante) e l'area di un rettangolo,
- se crediamo che questa inadeguatezza sia dovuta ai programmi ufficiali, ai libri di testo o agli insegnanti,
- se crediamo che il problema sia troppo difficile per gli allievi ai quali è stato proposto, cercheremo di "spiegare" il percorso da seguire alla maggior parte degli allievi in difficoltà, per poi scoprire poco dopo che la situazione non è migliorata.
A questo proposito, le stesse osservazioni si ritrovano nell'analisi dei risultati dei problemi Il terreno di Francesco (11.II.16), L'orto (I) (26.II.12), L'orto (II) (26.II.15) dove, invece di rettangoli con una dimensione costante, abbiamo a che fare con triangoli della stessa "altezza" la cui proporzionalità tra la misura della "base" e quella dell'area non è percepita.
La sezione seguente propone alcune attività per esplorare la ricchezza di questa situazione, dove si conoscono solo le misure delle aree di 5 dei 9 rettangoli.
Esempi di attività per un percorso didattico con la classe
Da sperimentare in classe, secondo le modalità stabilite dall'insegnante; con trasmissione di una descrizione e commenti per rendere conto dell’opportunità di proporre l’attività per la costruzione di saperi (indicati in corsivo).
Una delle ipotesi per spiegare l'ostacolo che incontrano gli allievi – e talvolta gli insegnanti – nel percepire i rapporti di proporzionali tra le aree e le misure di lunghezze dei rettangoli è legata alla mancanza di dati sulle misure di lunghezza (dimensione 1D) nella figura. I cinque numeri indicati sono misure di area (dimensione 2D) ed è necessaria una riflessione preliminare per rendersi conto che queste cinque misure non specificano il rapporto tra le due dimensioni di ciascun rettangolo.
a) Ritornare alla figura chiedendo che ogni allievo la disegni su carta a quadretti per facilitarne la costruzione, scegliendo il quadrato della quadrettatura come unità di area partendo, ad esempio, dalla linea orizzontale inferiore su cui sono allineati i tre rettangoli di area 18, 15 e 20, e dalla linea verticale sinistra su cui sono allineati i tre rettangoli della prima colonna di area 18, 15 e 20. (Questa attività di disegno viene svolta collettivamente, con numerose interazioni, sotto la guida dell'insegnante.)
Primo sapere di base: queste due rette sono perpendicolari. Secondo sapere: quando si tratta di disegnare un terzo lato orizzontale del rettangolo in basso a sinistra: Ci sono diversi rettangoli di area 18, un numero infinito! - oppure - si può scegliere qualsiasi numero per esprimere la dimensione verticale di questo rettangolo (larghezza o lunghezza).
Se, ad esempio, scegliamo 3 come distanza tra le prime due rette orizzontali (in lati del quadrato della quadrettatura) o misura verticale del lato del primo rettangolo, l'altra dimensione orizzontale viene determinata: 6, perché 3 x 6 = 18.
Ripasso delle nozioni di distanza tra due rette parallele, di misure di lunghezza (1D): 3 e 6, di misure di area (2D): 18, della formula per l'area di un rettangolo e le due unità di misura utilizzate, ecc.
Le dimensioni degli altri tre rettangoli sono definite come segue: 9 = 1,5 x 6; 15 = 3 x 5; e 20 = 3 x 20/3.
Le aree degli altri due rettangoli nella prima riga: 7,5 e 10, possono essere calcolate dalle dimensioni precedentemente scoperte o per proporzionalità: le aree dei rettangoli inferiori sono proporzionali a quelle dei rettangoli superiori, con il rapporto 9/18 = 1/2 o 18/9 = 2.
Per la linea centrale, le procedure sono le stesse. In base alla prima scelta di 3 come distanza tra le prime due linee orizzontali (sul lato quadrato della griglia), troviamo la sua dimensione verticale dall'area data del suo terzo rettangolo, 17, e dalla lunghezza del terzo rettangolo della terza linea, 20/3 che ci permette di ottenere 17/(20/3) = 17 x (3/20) = 51/20 = 2,55
Oltre ai saperi nell’ambito della geometria, ci sono quelli dell'aritmetica: rapporto tra due numeri naturali, numeri razionali in forma decimale o come frazione per quelli che non sono decimali, semplificazione delle frazioni, moltiplicazione di frazioni, numeri o frazioni inversi, proporzionalità, ecc.
b) Confronto delle figure dei nove rettangoli in base a diverse scelte di una delle due misure (ogni allievo fa una scelta diversa di una delle due misure di uno dei cinque rettangoli; un confronto dovrebbe far apparire diversi rapporti tra le dimensioni dei rettangoli (alcuni più "allungati" di altri) ma sempre con le stesse aree la cui somma è sempre la stessa: (9 + 7,5 + 10) + (15,3 + 12,75 + 17) + (18 + 15 + 20) = 124,55 (in quadrati della quadrettatura).
Saperi: rettangoli con le medesime aree ma non simili (similitudine), conservazione dei rapporti di proporzionalità tra le aree dei rettangoli da una riga all'altra o da una colonna all'altra.
c) Domande o sviluppi (esempi)
- Il rapporto tra le aree dei rettangoli della prima riga e quelli della terza riga è 2. Il rapporto tra le aree dei rettangoli della prima riga e quelli della seconda riga è 1,7. Questi due rapporti possono essere utilizzati per calcolare il rapporto tra le aree dei rettangoli della seconda riga e quelli della terza riga?
- Se aggiungessimo una quarta colonna di tre rettangoli alla figura dei nove rettangoli, oltre alle cinque aree indicate, quanti ne dovremmo avere almeno per trovare l'area totale?
- Uno dei nove rettangoli potrebbe essere quadrato?
- ...
d) Altri problemi che coinvolgono rettangoli giustapposti che utilizzano le dimensioni di queste figure e le loro aree: Il tavolo da giardino (15.I.12), La scatola (11.F.09), Pavimento di legno(23.I.14)