
Banque de problèmes du RMT
sd153-fr
 |
Banque de problèmes du RMTsd153-fr |
|
Envoyer une remarque ou une suggestion
Déterminer le nombre de losanges nécessaires pour construire un hexagone de côté 12 fois celui d'une losange.
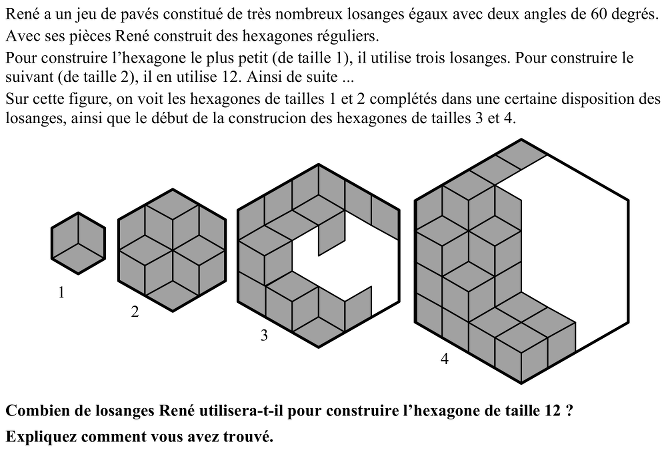
- Comprendre que si on prend comme unité de longueur un côté d’un losange, les longueurs des côtés des hexagones successifs sont 1, 2, 3, 4, ... et correspondent « aux tailles ». ». Prendre un losange comme unité d’aire.
- Se rendre compte que, quelle que soit la disposition des losanges, le nombre de losanges ne change pas pour un hexagone d’une taille donnée, car son aire est donnée.
- Compléter les hexagones de tailles 3 et 4 et compter leurs losanges : 27 et 48.
- Examiner la suite des nombres de losanges : 3, 12, 27, 48, ... et chercher une règle de passage d’un terme au suivant par conjectures et vérifications. Par exemple, la multiplication par 4 qui permet de passer de 3 à 12 ne convient plus pour le passage de 12 à 27.
Le calcul des différences d’un nombre au suivant fait en revanche apparaître une régularité intéressante : une augmentation du nombre de losanges, de 6 en 6, d’une taille à la suivante :

ce qui permet de conjecturer que de 12 = 3 + 3 + 1 x 6 ; 27 = 12 + 3 + 2 x 6 ; 48 = 27 + 3 +3 x 6 et que le terme suivant pourrait être 75 = 48 + 3 + 4 x 6.
- Se rendre compte alors qu’il est nécessaire de vérifier cette conjecture sur l’hexagone de taille 5, puis de taille 6, en dessinant les figures correspondantes ou en « prolongeant » celle de taille 4, ... (cette vérification nécessite toutefois des dessins précis, à la règle pour pouvoir y marquer les losanges et les dénombrer).
La conjecture vérifiée sur quelques exemples, elle peut être utilisée pour arriver à l’hexagone de taille 12, par le calcul de tous les termes successifs : 108 = 75 + 3 + 5 x 6 ; 147 ; 192 ; 243 ; 300 ; 363 ; 432
Ou : trouver d’autres régularités dans les différences successives qui sont des produits des nombres impairs multipliés par 3. (9 = 3 x 3, 15 = 5 x 3, 21= 7 x 3, 27 = 9 x 3, ...)
Ou : factoriser les nombres de la suite en fonction de la taille de l’hexagone :
taille : 1 2 3 4 5 ... nb. losanges: 3=3 x 1 12=3 x 2 x 2 27=3 x 3 x 3 48=3 x 4 x 4 75=3 x 5 x 5 ...
On arrive ainsi au lien « fonctionnel » entre la taille (n) de l’hexagone et le nombre de losanges n —> 3 x n2, ce qui conduit, pour n = 12 à 3 x 122 = 3 x 144 = 432, sans passer par les termes successifs.
Remarque : ce lien est « naturel » pour les élèves qui savent qu’en doublant les dimensions de l’hexagone de taille 1 (ou de toute autre figure), on multiplie son aire par 4 = 22 ; en les triplant on multiplie son aire par 9 = 32 ; en les multipliant par 12, on multiplie l’aire par 122.
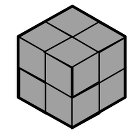
Ou : faire un remplissage « régulier » de l’hexagone (où tous les losanges de même orientation sont regroupés) conduisant à la représentation d’un cube en perspective cavalière : le cube présente 3 faces identiques, pavées par n x n losanges, d’où le nombre 3n2 et la réponse 3 x 122 = 432.
addition, multiplication, carré, suite, proportions, losange, hexagone, pavage
Les résultats n'ont pas été conservés ou ne sont pas encore disponibles.