
Banca di problemi del RMT
sd153-it
 |
Banca di problemi del RMTsd153-it |
|
Envoyer une remarque ou une suggestion
Determinare il numero di esagoni necessari per costruire un esagono con il lato 12 volte maggiore di quello dell’esagono piccolo.
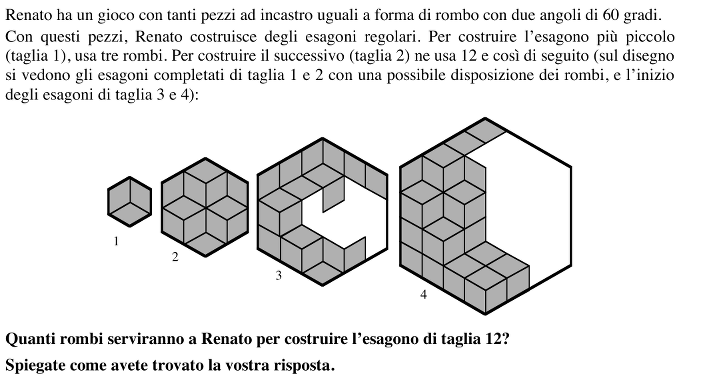
- Capire che se si prende come unità di misura delle lunghezze un lato del rombo, la lunghezza dei lati degli esagoni aumenta di 1 ogni volta che l’esagono ingrandisce: le misure dei lati degli esagoni successivi sono 1, 2, 3, 4, ... e corrispondono alle «taglie». Prendere un rombo come unità d’area.
- Rendersi conto che comunque si sistemino i pezzi a forma di rombo, il numero necessario a formare un esagono di una certa taglia, non cambia, poiché la sua area è data.
- Completare le figure 3 e 4 e contare i rombi necessari: 27 e 48.
- Esaminare la successione dei numeri di rombi: 3, 12, 27, 48, ... e cercare di capire la relazione tra due numeri successivi tramite congetture e verifiche.
Per esempio, da 3 a12 si passa moltiplicando per 4, cosa che non funziona per passare da 12 a 27! Il calcolo delle differenze di un numero e del successivo fa, al contrario, apparire una regolarità interessante: un aumento di 6 in 6:
«taglia»: 1 2 3 4 ... Successione dei numeri: 3 12 27 48 ... Differenze: 9 15 21
Cosa che permette di congetturare che da 12 = 3 + 3 + 1 x 6; 27 = 12 + 3 + 2 x 6; 48 = 27 + 3 +3 x 6 il termine seguente potrebbe essere 75 = 48 + 3 + 4 x 6.
- Capire quindi che è necessario verificare questa congettura con l’esagono successivo e pertanto disegnarlo (con il righello possibilmente) e contare i pezzi: 48; rendersi conto allora che è necessario verificare questa congettura sull’esagono di taglia 5, poi di taglia 6, disegnando le figure corrispondenti, o «prolungando» quello di taglia 4, ...(questa verifica necessita tuttavia di disegni precisi, con il righello, per poter indicare i rombi e contarli.
La congettura verificata su qualche esempio può essere utile per arrivare all’esagono di taglia 12, con il calcolo di tutti i termini successivi: 108 = 75 + 3 + 5 x 6, 147; 192; 243; 300; 363; 432.
Oppure: trovare altre regolarità nelle differenze successive che sono dei prodotti di numeri dispari moltiplicati per 3, come (9 = 3 x 3, 15 = 5 x 3, 21= 7 x 3, 27 = 9 x 3, ...
Oppure: fattorizzare i numeri successivi e fattorizzare i numeri della successione in funzione della taglia dell’esagono:
taglia: 1 2 3 4 5 ... n. rombi: 3 = 3x1 12 = 3x2x2 27 = 3x3x3 48 = 3x4x4 75 = 3x5x5 ...
Si perviene così ad un legame «funzionale» tra la taglia (n) di esagoni e il numero di rombi n —> 3 x n2, cosa che conduce, per n = 12 a 3 x 122 = 3 x 144 = 432, senza passare per i termini successivi.
Osservazione: questo legame è «naturale» per gli allievi che sanno che, raddoppiando le dimensioni dell’esagono di taglia 1 (o di qualunque altra figura), se ne moltiplica l’area per 4 = 22; triplicando le dimensioni, se ne moltiplica l’area per 9 = 32; moltiplicando per 12, si moltiplica l’area per 122.
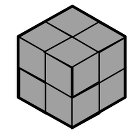
Oppure: fare un riempimento «regolare» dell’esagono (nel quale tutti i rombi della stessa orientazione sono raggruppati) che conduce alla rappresentazione di un cubo in prospettiva: il cubo presenta 3 facce identiche, pavimentate con n x n rombi, da cui il numero 3n2 e la risposta 3 x 122 = 432.
addizione, moltiplicazione, elevamento a potenza, successioni, rombo, esagono
I risultati non sono stati salvati o non sono ancora disponibili.