La rosace de Julie (II)

Identificazione

Rally: 15.II.07 ; categorie: 5, 6 ; ambito: GP
Famiglie:

• CA - Comparer des aires
• CA/D - Comparer des aires par découpage
• DEC - Découper et/ou assembler des figures

Envoyer une remarque ou une suggestion

Sunto

Décomposer une surface en carrés et triangles et comparer les aires de deux parties.

Enunciato

Compito per la risoluzione e saperi mobilizzati

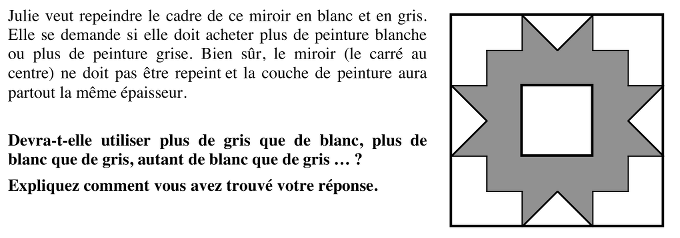
- Comprendre que le carré du milieu n’intervient pas dans la comparaison des aires.

- Comprendre que la surface blanche à couvrir peut être décomposée en plusieurs surfaces.

- Comprendre qu’il est possible de comparer des aires sans les mesurer ou les calculer avec des unités conventionnelles.

- Voir des décompositions possibles de chaque figure en ajoutant des traits dans le carré : déterminer l’unité de mesure commune (un carré ou un triangle) ; compter le nombre de carrés (16) ou de triangles (16) dans chacune des deux parties à colorier ; comparer ces deux nombres et reconnaître l’égalité des aires à couvrir.

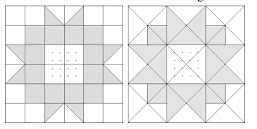
- Voir qu’il est possible d’ajouter des lignes dans la partie grisée pour obtenir des carrés ; réaliser l’appariement géométrique entre ces quatre carrés et les quatre triangles clairs ; huit plus grands carrés à colorier apparaissent alors, quatre blancs, quatre gris ; constater l’égalité des aires.

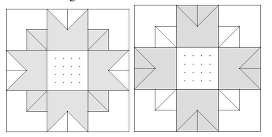
- Tracer les médianes du grand carré ; prolonger les lignes intérieures pour faire apparaître des formes identiques aux quatre formes claires de coin ; réaliser des appariements géométriques entre ces formes et réaliser des appariements entre les triangles blancs et les triangles gris ; constater l’égalité des aires.

Nozioni matematiche

aire, unité de mesure

Risultati

15.II.07

Points attribués sur 123 classes de Suisse romande:

Selon les critères déterminés lors de l’analyse a priori :

• 4 points: Solution complète (égalité des aires, autant de peinture grise que de blanche, ...) avec explications correctes, par exemple avec le dessin des décompositions prises en compte
• 3 points: Solution correcte, avec explications incomplètes ou dessin peu clair
• 2 points: Solution correcte sans explication
  oppure erreur de comptage mais explication correcte
  oppure prise en compte du miroir avec réponse cohérente « plus de blanc » et explications correctes
• 1 point: Début de recherche cohérente
• 0 point: Incompréhension du problème, ou réponse « autant de blanc que de gris » fondée sur un comptage qui ne tient pas
compte de la grandeur des pièces.