Le foulard

Identification

Rallye: 14.II.05 ; catégories: 3, 4, 5 ; domaine: GP
Familles:

• CA - Comparer des aires
• CA/D - Comparer des aires par découpage
• RO - Paver une figure de manière optimale

Envoyer une remarque ou une suggestion

Résumé

Dans un carré pavé de triangles, rectangles et carrés, rechercher les rapports entre les côtés et les aires des différentes parties.

Enoncé

Tâche de résolution et savoirs mobilisés

Analyse a priori

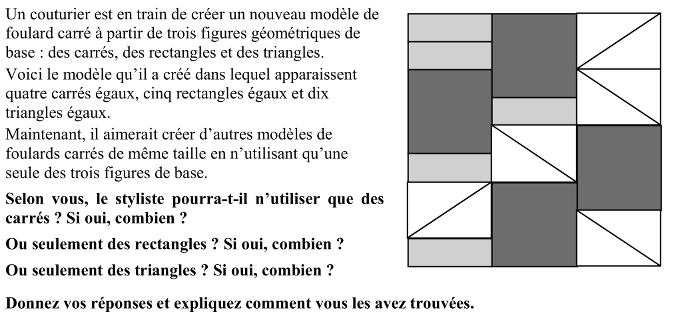
Observer le dessin et confronter les bandes qui divisent le grand carré, de même aire mais constituées de figures différentes, en formes et nombres.

Déduire, par confrontation des bandes deux à deux :

- un carré est équivalent à trois rectangles (confrontation entre la bande de gauche et la bande centrale)

- un triangle rectangle est équivalent à un rectangle (puisque quatre rectangles et quatre triangles sont équivalents, comme on l’observe en comparant la bande de gauche et la bande de droite)

Déduire du dessin et des considérations sur les équivalences entre figures que le foulard peut être recouvert en utilisant seulement des carrés (il en faut 9) ou seulement des rectangles (il en faut 27).

Puisque les triangles sont équivalents aux rectangles, on pourrait penser que le foulard peut être recouvert aussi par 27 triangles. Mais il n’est pas possible d’utiliser seulement ces triangles : ils devraient en effet être unis deux à deux par leurs hypoténuses pour former des rectangles « doubles » (équivalant à deux petits rectangles) ; pour le pavage et on ne pourrait en placer que 13 au maximum (correspondant à 26 petits rectangles). Il resterait alors une partie vide du foulard (équivalente à un rectangle).

Ou : procéder de manière empirique, par exemple par découpage précis des pièces et par pavage ou, par mesurage des côtés pour déterminer les rapports entre les côtés.

Notions mathématiques

côté, aire, lungueur, rectangle, triangle, carré, mesure, rapport, pavage

Résultats

14.II.05

Sur 249 classes de 5 sections (RZ, PR, GE, PG, LO) ayant participé à l'épreuveII du 14e RMT

Selon les critères déterminés lors de l’analyse a priori :

• 4 points: Réponses correctes (Oui, avec 9 carrés ; Oui, avec 27 rectangles ; Non avec les triangles) et bien justifiées (avec argumentation, dessins, …)
• 3 points: Réponses correctes sans explication ou avec dessins imprécis
• 2 points: Réponses 9 carrés et 27 rectangles avec justifications, mais erreurs ou sans la réponse concernant les triangles
• 1 point: Une seule réponse correcte donnée et justifiée ou tentatives qui révèlent une compréhension initiale du problème
• 0 point: Incompréhension du problème

Procédures, obstacles et erreurs relevés

Stratégies de résolution les plus fréquentes :

- Comparaison et équivalences entre les figures ;

- Découpage et pavage du carré de base (moins utilisé que la précédente)

Erreurs les plus courantes

Les erreurs les plus fréquentes proviennent de reproductions erronées généralement sur papier quadrillé.

Les enfants se réfèrent notamment à des rectangles et à des triangles rectangles en prenant en compte « l’image mentale » de ces figures géométriques plutôt que les modèles proposés (la situation réelle). Le problème devient : recouvrir le carré de base avec des carrés égaux, avec des rectangles tous les mêmes et avec des triangles rectangles égaux.

On met en évidence dans certaines copies de catégorie 3 la non-reconnaissance des formes (confusion entre carré et rectangle). On leur attribue, en pourcentage variable selon les sections, aucun point pour une incompréhension du problème (par exemple : dessin ou chevauchement de tous les types de figures pour paver le même foulard). Concernant ce dernier point, on peut se demander si l’incompréhension du problème ne serait pas lié au texte du problème.

D’après les copies examinées, il semble se dégager les points suivants :

1) L’observation visuelle est privilégiée pour compter les formes avec la représentation iconique plutôt que l’activité manipulatrice de recadrage et de chevauchement.

2) il est difficile d’identifier une unité de mesure ;

3) il est difficile de reconnaître l’équivalence des figures (par exemple : équivalence 1 carré vaut 3 rectangles ou même 2 triangles + 1 rectangle...) ;

Le problème était difficile, en particulier pour les catégories 3 et 4 où les 3 ou 4 points sont attribués, comme nous l’avons vu, à un petit nombre de copies. En revanche, on constate une augmentation considérable des réussites dans la catégorie 5.

Exploitations didactiques

En ce qui concerne la construction du concept d’aire, le problème pourrait être utilisé lors d’une phase déjà avancée du processus car il représente une synthèse entre pôle géométrique, pôle grandeur et pôle numérique (Douady-Perrin-Glorian 1989), même si ce dernier n’apparaît pas de manière évidente.

C’est précisément à cette situation que pourraient être liées les difficultés qui sont apparues, en particulier dans les catégories 3 et 4, en raison d’une utilisation « prématurée », peut-être pas dans un sens absolu, mais par rapport au travail effectué dans les classes. Le fait que l’énoncé soit long et complexe peut avoir causé des malentendus et des difficultés de compréhension.

Pour aller plus loin

Après cette analyse, le problème a été proposé dans la classe de quatrième de Clara Bisso, une classe où un groupe avait travaillé sur « Le foulard » l’année précédente lors du test du 14ème édition du RMT (mauvaise reproduction sur papier). Après l’épreuve, le problème avait été proposé à toute la classe, pour la correction qui suit chaque test, et des solutions correctes avaient émergé obtenues avec un raisonnement sur la comparaison / équivalence des figures.

Dans cette nouvelle phase, le problème a été donné à une classe organisée en 6 groupes, le problème semblait être une nouveauté pour les enfants. Deux groupes ont trouvé la solution correcte, un groupe s’est perdu avec les triangles (comme il restait de l’espace, ils ont « arrondi » par excès le nombre de triangles), un autre groupe a reproduit la figure de manière erronée en faussant ses mesures (l’image mentale mentionnée ci-dessus), deux groupes d’élèves faibles ont eu des difficultés à comprendre le texte.

Tous les groupes ont eu recours à la reproduction ou à la reproduction suivie du découpage (avec une certaine imprécision). Au cours de la mise en commun, « le voile s’est déchiré » et les élèves ont commencé à comparer les figures pour identifier des équivalences.

Quelques observations

Les résultats de l’épreuve et les difficultés apparentes rencontrées par les élèves de quatrième, malgré tout le travail effectué avec eux sur l’aire, conduisent à plusieurs questions à la fois sur l’énoncé, comme précédemment évoqué, et sur les aspects cognitifs liés à la construction du concept d’aire et suggère de ne pas sous-estimer des aspects fondamentaux importants tels que la comparaison entre les objets et l’équivalence des figures. Des aspects qui nous semblent trop souvent considérés comme « intuitivement simples ».

Le groupe de travail (GTGP) proposera un nouvel énoncé visant à limiter les difficultés d’interprétation et les ambiguïtés et proposera une nouvelle version du problème dans différentes classes.

C’est ainsi que le groupe a procédé avec le problème Les deux lettres dont une nouvelle version de l’énoncé est testée.