Biscuits

Identification

Rallye: 14.II.07 ; catégories: 4, 5, 6 ; domaine: GP
Familles:

• CA - Comparer des aires
• CA/P - Comparer des aires sur un quadrillage

Envoyer une remarque ou une suggestion

Résumé

Comparer la grandeur de f1gures dessinées sur un réseau triangulaire en effectuant les approximations nécessaires.

Enoncé

Tâche de résolution et savoirs mobilisés

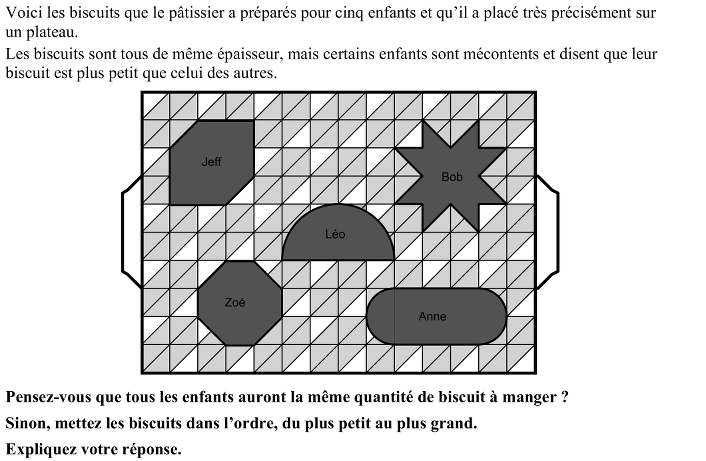
Analyse a priori de la tâche:

- Déterminer la grandeur en jeu pour trouver la part de biscuit de chacun : écarter les angles (forme), le nombre de côtés ou sommets et le périmètre ; opter pour l’aire des figures (ou le volume vu que les biscuits ont tous la même épaisseur)

- Trouver un moyen de comparer les aires : constater que les tentatives de superposition ou de découpage et reconstitutions ne donnent pas de résultats probants ; penser à utiliser la trame du plateau pour « paver » les formes (en carrés, triangles, …)

- Imaginer ou dessiner la trame du plateau sur les figures, choisir une unité et procéder au comptage pour les figures « pavables » (En carrés on obtient 8 pour Jeff et Bob, 7 pour Zoé)

- Pour les figures non « pavables », constater que dans la figure d’Anne il y a 6 carrés entiers et 4 quarts de disques (quatre demi-carrés et quatre petites parties de disques), ce qui équivaut à une mesure de plus de 8 carrés. La figure de Léo est inscrite dans un rectangle de 8 carrés, en retirant 2 demi-carrés et d’autres parties de carrés, on arrive à une mesure inférieure à 7 carrés.

- Établir le classement. Par exemple, en exprimant les aires en carrés : Léo (< 7), Zoé (7), Jeff et Bob (8), Anne (>8).

Notions mathématiques

aire, approximations, comptage, addition

Résultats

14.II.07

Points attribués sur 166 classes de Suisse romande:

Selon les critères déterminés lors de l’analyse a priori :

• 4 points: Le classement complet (Léo (< 7), Zoé (7), Jeff et Bob (8), Anne (>8)) avec explications claires
• 3 points: Le classement correct des cinq biscuits avec explications peu claires
  ouune interversion due à une erreur de la détermination de l’aire d’un biscuit, mais avec explications claires
• 2 points: Le classement avec une seule interversion avec explications peu claires
  ou deux interversions dues à une erreur de la détermination de l’aire de deux biscuits, mais avec explications claires
• 1 point: Début de pavage, mais sans utiliser la même unité ou avec plus de deux erreurs
• 0 point: Incompréhension du problème, mesurage de périmètres, comptage des sommets, …

Bibliographie

Mecacci A. Analisi e considerazioni emerse dalla sperimentazione dei problemi “Rettangoli su carta quadrettata” e “Biscotti". Allegato I de: Bisso C. Grugnetti L. Gruppo geometrie piana. Geometria plane nell'ARMT / La géometrie plane dans l’ARMT. In Gazzzetta del Transalpino/ Gazette de Transalpie no 15, pp 141 - 155