
Banca di problemi del RMT
sd254-it
 |
Banca di problemi del RMTsd254-it |
|
In una successione in cui si alternano i termini 5 e -2, trovare il numero dei termini necessari affinché la somma vada da 15 a 80.

- Riconoscere che c’è una «sovrapposizione» di allungamenti e accorciamenti della barba che possono tradursi in un aumento di 3 cm da un mattino al mattino successivo.
- Comprendere che il numero di giorni cercato corrisponde al numero di volte che si deve aggiungere 3 a 15 per oltrepassare 80 (per es., calcolare: 80-15=65 poi 65:3=21,66...) e concludere che Gargantua dovrà attendere 22 giorni.
Oppure: annotare, giorno per giorno, la lunghezza della barba
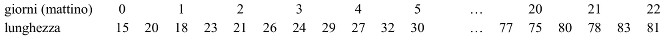
Oppure: dopo aver compreso che l’allungamento da un mattino al successivo è di 3 cm, procedere con una divisione (80:3=26,66...) per dedurre che occorreranno 27 giorni; calcolare il numero dei giorni (5) che gli saranno occorsi per arrivare a 15 cm (15:3 = 5) e infine sottrarre: 27-5=22.
aritmetica
Points attribués sur 92 classes de Suisse romande:
| Categoria | 0 | 1 | 2 | 3 | 4 | Nb.classi | Media |
|---|---|---|---|---|---|---|---|
| Cat 4 | 7 (16%) | 1 (2%) | 6 (14%) | 10 (23%) | 19 (44%) | 43 | 2.77 |
| Cat 5 | 2 (4%) | 2 (4%) | 3 (6%) | 15 (31%) | 27 (55%) | 49 | 3.29 |
| Totale | 9 (10%) | 3 (3%) | 9 (10%) | 25 (27%) | 46 (50%) | 92 | 3.04 |
| Si ricorda che il problema è stato affrontato nelle condizioni particolari del RMT: intera classe, allievi in completa autonomia, da 5 a 7 problemi da risolvere, un solo foglio risposta per problema. | |||||||
(c) ARMT, 2005-2024