
Banca di problemi del RMT
sd273-it
 |
Banca di problemi del RMTsd273-it |
|
Envoyer une remarque ou une suggestion

- Cercare quali possono essere i bambini aventi la stessa altezza: Sara e Eddy non possono essere della stessa altezza, restano dunque due possibilità: Ugo-Sara e Leo-Edy o Ugo-Edy e Leo-Sara.
- Nella prima ipotesi, la differenza di 20 cm (135 – 115) tra Sara e Ugo sarà compensata da una differenza di 4 cre (7 – 3), cosa che porterà ad avere 5 cm per 1 cre, e la differenza di 15 cm (145 – 130) tra Edy e Leo sarà compensata dalla differenza di 3 cre (6 – 3), cosa che dà ancora 5 cm per 1 cre.
- Nella seconda ipotesi, la differenza di 5 cm (135 – 130 tra Sara e Leo sarà compensata da una differenza di 3 cre (6 – 3), cosa che darà 5/3 cm per 1 cre , e la differenza di 30 cm (145 – 115) tra Edy e Ugo sarà compensata dalla differenza di 4 cre (7 – 3), cosa che darà 7,5 cm per 1cre, in contraddizione con la precedente.
La seconda ipotesi è da respingere e la prima conduce alla corrispondenza 1 cre = 5 cm.
Oppure: procedere in maniera sistematica, attribuendo dei valori successivi al "cre", in cm, calcolare le altezze dei bambini quando sono cresciuti come indicato, e osservare i risultati:
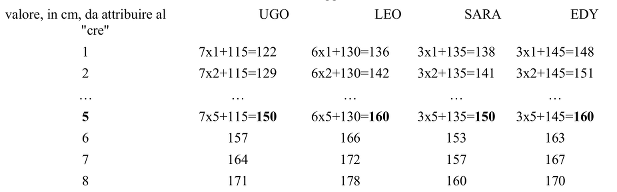
- Comprendere che, se si continua a dare altri valori al "cre", non sarà più possibile avere due coppie di persone della stessa altezza: Sara e Edy avranno sempre la stessa differenza di altezza, Leo ha superato Sara “tra 1 e 2 cm” e Edy dopo 5 cm, Ugo ha superato Sara dopo 5 cm e Edy tra 7 e 8 cm.
Oppure: procedere facendo dei tentativi a caso, senza peraltro arrivare all’unicità della soluzione.
I risultati non sono stati salvati o non sono ancora disponibili.