
Banque de problèmes du RMT
sd30-fr
 |
Banque de problèmes du RMTsd30-fr |
|
Déterminer le poids de trois pots de confiture de tailles différentes (P, M, G) sachant que. de façon illustrée, 4P + 4M + G = 5 kg; 7P + 2G = 5 kg et 7P + 6M = 5 kg.
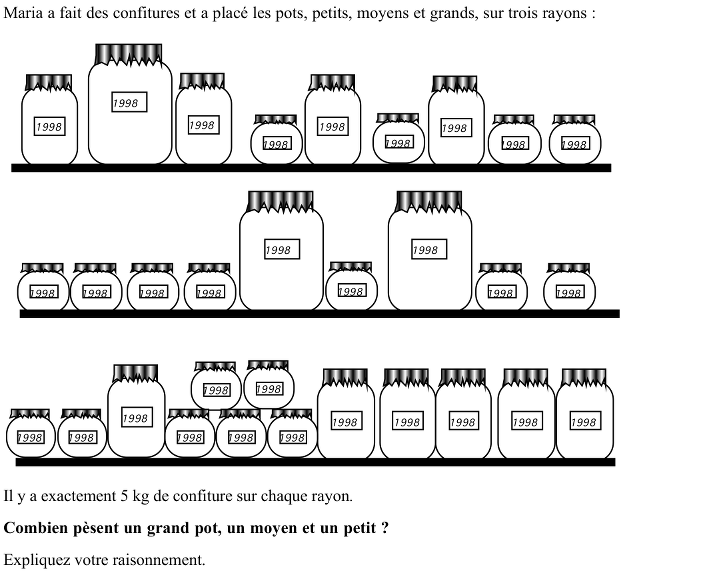
Observer les dessins des trois rayons et les pots; constater qu'il y a trois sortes de pots, petits (P) moyens /M) et grands(G) et comprendre que le poids de chaque sorte de pots est le même pour chacun des rayons. (La phrase de l'énoncé Il y a exactement 5 kg de confiture sur chaque rayon doit évidemment être comprise comme Il y a exactement 5 kg de pots, tous pleins de confiture sur chaque rayon)
Passer dans le registre numérique et établir les trois relations 4P + 3M + G = 5 (en kg), 7P + 2G (en kg) et 7P + 6M = 5 (en kg) et en tirer aussi les relations entre deux des trois rayons : 4P + 3M + G = 7P + 2G ; 4P + 3M + G = 7P + 6M ; 7P + 2G = 7P + 6M.
En l'absence de connaissances algébriques (il s'agit de résoudre système de trois équations du premier degré à trois inconnues) il y a deux manières de résoudre le problème, par des échanges successifs et substitution reposant sur les relations d'équivalence et leurs propriété ou par des essais et vérifications.
- Par échanges et substitution, selon l'image des plateaux d'une balance en équilibre, l'opération la plus évidente est de retirer 7 petits pots des deux rayons inférieurs, pour arriver à l'équivalence 2G = 6M puis, par une simplification par 2, à 1G = 3M
En retirant 4P et 1G des deux rayons du haut on arrive à 4M = 1G + 3P, puis par substitution de 1G par 3M (tiré de la comparaison précédente) sur le rayon du milieu on arrive à 4M = 3M + 3P, puis finalement en retirant 3M des deux rayons du haut on obtient le relation 1M = 3P.
On peut alors substituer les G et les M par des P et, pour chacun des trois rayons on arrive à 25P = 5 (en kg) pour en tirer la masse d'un P = 5/25 = 0,2 (en kg) puis la masse d'un M = 3 x 0,2 = 0,6 (en kg) et la masse d'un G = 3 x 0,6 = 1,8 (en kg).
- La méthode par essais nécessite plusieurs étapes. Tout d'abord trouver des masses pour P, M et G qui satisfont l'égalité avec 5 kg pour l'un des trois rayons; (Par exemple pour le rayon du milieu en choisissant P = 0,1 on trouve G = (5 - 7 x 0,1 /2 = 2,15); puis appliquer ces deux valeurs sur un deuxième rayon pour trouver la troisième valeur (Selon l'exemple précédent, on aurait sur le premier rayon 4 x 0,1 + 2,15 + 4 M = 5, ce qui donnerait M = (5 - 0,4 - 2,15)/ 4 = 0,5875) et enfin vérifier si les trois valeurs vérifient l'égalité du troisième rayon. (Selon l'exemple précédent, il faudrait vérifier l'égalité du troisième rayon: 7P + 6M = 7 x 0,1 + 6 x 0,5875 = 4,225, voir que cette somme est différente de 5 et en conclure qu'il faut rejeter le premier essai P = 0,1).
Par bonheur, un essai è partir de P = 0,2 permet de vérifier les trois égalités. Mais cette méthode, naturelle, est longue et très difficile à mener sur toutes les étapes.
addition, multiplication, équation, substitution, équivalence
Sur 127 copies de quatre sections
| Catégorie | 0 | 1 | 2 | 3 | 4 | Nb. de classes | Moyenne |
|---|---|---|---|---|---|---|---|
| Cat 6 | 46 (70%) | 5 (8%) | 1 (2%) | 10 (15%) | 4 (6%) | 66 | 0.8 |
| Cat 7 | 20 (50%) | 2 (5%) | 0 (0%) | 11 (28%) | 7 (18%) | 40 | 1.58 |
| Cat 8 | 4 (19%) | 2 (10%) | 1 (5%) | 5 (24%) | 9 (43%) | 21 | 2.62 |
| Total | 70 (55%) | 9 (7%) | 2 (2%) | 26 (20%) | 20 (16%) | 127 | 1.35 |
| Rappel: Le problème est résolu dans les conditions particulières du RMT: classe entière, élèves en autonomie complète, 5 à 7 problèmes à résoudre, une seule feuille de réponses par problème. | |||||||
L'observation de ce tableau montre à l'évidence que le problème n'est pas adapté aux classes de catégorie 6: 70% d'incompréhension du problème et une moyenne de 0,8 point. Il est même "très difficile" pour des classes de catégorie 7.
Une analyse a posteriori de 127 copies de ce problème est décrite dans l'article cité en bibliographie. En voici quelques extraits:
1. Réponses obtenues par essais
a) On s'intéresse au premier rayon et on ignore les autres. On procède par essais successifs en ajustant à chaque fois la masse des trois récipients, jusqu'à déterminer des valeurs compatibles avec la quantité de confiture présente sur ce rayon :
Le grand pèse 1450 gr. Le moyen pèse 587,5 g. Le petit pèse 300 g. Nous avons additionné et multiplié des nombres possibles jusqu'à ce que nous arrivions au résultat final.
Les grands pots pèsent 7,5 hg, les moyens 5,75 hg, les petits 5 hg. J'ai essayé en disant que les grands pesaient 1 kg, et les petits seulement 5 hg et en additionnant ça n'allait pas, alors j'ai commencé à enlever des hg aux grands jusqu'à ce que ce soit juste. J'ai fait la même chose avec les moyens.
Dans quelques cas, la masse d'un pot est fixée, celle du grand en général, et la masse des deux autres est déterminée en se référant à la décomposition de 5 comme somme de nombres naturels ( 2 + 2 + 1 ; 2 + 3 ; 4 + 1) :
Grand pot 2 kg, moyen 500 g, petit 250 g ... On a trouvé cette solution en décomposant le nombre 5 : [5 kg = 2 kg + (500 x 4) g + (250 x 4) g ]
Le petit pot pèse 0,15 kg, le pot moyen pèse 0,60 kg, le grand pot pèse 2 kg. Pourquoi ? Parce que la somme des pots sur le premier rayon fait 5 kg [5 kg = 2 kg + 3 kg = 2 kg + (600 x 4)g + (150 x 4)g ]. Le petit pot : 50 g; le moyen: 200 g; le grand : 4 kg [5 kg =4 kg + 1 kg = 4 kg + (200 x 4) g + (50 x 4) g ]
On observe que le contrôle sur les autres rayons est absolument ignoré, comme si les informations qu'on pourrait en retirer étaient des données inutiles ou surabondantes. On se contente de la première réponse, influencé par le fait que, d'habitude, une fois qu'on a trouvé une solution < b) On procède, comme dans le cas précédent, par essais sur un rayon, mais cette fois, on effectue aussi un contrôle sur les deux autres, mais en oubliant une des variables en jeu.
On admet que la masse totale de 5 kg sur chaque rayon peut varier :
Le grand pot pèse 1,5 kg, le pot moyen pèse 0,5 kg et le petit pot pèse 0,375 kg. Sur le premier rayon: 1,5 + 0,5 + 0,5 + 0,5 + 0,5 + 0,375 + 0,375 + 0,375 + 0,375 = 5 kg. Sur le deuxième rayon: 0,375 + 0,375 + 0,375 + 0,375 + 0,375 + 0,375 + 0,375 + 1,5 + 1,5 = 5,625 kg. Sur le troisième: Tot. 5,625 kg
On sent la nécessité d'une hypothèse selon laquelle la masse des pots varierait d'un rayon à l'autre :
HYPOTHÈSE: Sur chaque rayon, les pots pourraient être différents ...
c) La solution correcte se détermine en procédant par tentatives plus ou moins organisées, en ajustant les masses et en contrôlant toutes les variables :
Au début, nous avons supposé que le grand vaut 2 kg, le moyen 0,500 kg et le petit 0,200. En modifiant le grand, chaque fois de 0, 1, on a trouvé 1,8. Puisque le grand est 1,8, nous avons augmenté le moyen de 0,050 gr et ainsi, on a obtenu 0,600 g
On a fait des essais. Grand: 1 kg; moyen : 500 g ; petit : 250 g et ceci n'allait pas bien; puis avec le grand : 1,88 kg; moyen: 460 g ; petit : 320 g et encore beaucoup d'autres. Et par hasard, le grand : 1800 g; moyen : 600 g; petit : 200 g
Quelquefois, le rappel de l'expérience concrète peut aider ...
J'ai vu qu'il y avait 7 petits pots sur le deuxième et sur le troisième rayon, ce qui a permis plusieurs essais, et quand j'ai com- pris, par la proportionnalité, que les petits pesaient 200 g ..·
...et, d'autres fois, c'est le hasard qui a un rôle déterminant :
Nous sommes partis de la deuxième colonne et par un pur hasard, nous avons remarqué que la date des grands pots est 1998 et nous avons pris le premier et le dernier chiffre pour dire que la masse des pots est 1,8.
2. Réponses fondées sur l'hypothèse que la masse du grand pot est le double de celle du moyen et que cette dernière est le double de celle du petit
Ceux qui ont donné ce type de réponse se sont probablement laissés fourvoyer par le dessin, sur lequel le rapport entre les capacités des pots grand-moyen et moyen-petit semble être vraiment de 2 à 1 :
On trouve encore des réponses obtenues par confrontations et essais, des réponses obtenues par confrontations et substitutions (du genre de la première procédure décrite dans l'analyse de la tâche) et une seule production d'une classe de catégorie 8 qui pose qui résout le système d'équation utilisant de manière appropriée le calcul algébrique.
Les auteurs de l'article qui décrit cette analyse a posteriori du problème ajoutent encore quelques observations:
Plus d'une fois, on a relevé les difficultés liés au concept de division. Chez certains élèves, c'est le modèle primitif de cette opération sur les nombres naturels, qui contraint en particulier le dividende à être toujours supérieur au diviseur, qui paraît encore bien enraciné : devant la nécessité d'exécuter une division dans laquelle le dividende et le diviseur sont dans la bonne, relation, les deux nombres sont intervertis avec désinvolture.
Dans certains cas, on a pensé à faire les calculs sans s'en préoccuper puis à interpréter les résultats de manière réaliste (le grand pot= 3333,3333333 g, le petit pot = 166,6666665 g) : il s'agit de cette aptitude, assez répandue et à ne pas ignorer d'un point de vue didactique, qui consiste à accepter sans critique, pour un problème scolaire des résultats qui seraient considérés comme impossibles dans une situation réelle.
Il est évident que ce problème, pour des classes de catégorie 8 ou 9, (13 à 15 ans) peut servir d'introduction à la résolution d'un système d'équations, ou les calculs littéraires sont précédés d'une formulation réthorique liée très étroitement aux manipulations d'objets sur les plateaux d'une balance qui maintiennent l'équilibre.
Les opérations concrètes et effectives permettent de donner du sens aux écritures formelles avec des x, y, ...
(c) ARMT, 1998-2024Exploitations didactiques
Bibliographie
C. Crociani, L. Doretti, L. Salomone. Un problème et son analyse didactique : les pots de confiture. In ACTES DES JOURNEES D'ETUDES SUR LE RMT (Vol. 1, 1e et 2e rencontres). RMT: Quels apports pour la didactique des mathématiques.pp 115-128. Brigue 1997-98, (1999). L. Grugnetti & F. Jaquet (Eds) Dipartimento di Matematica, Università di Parma & Institut de recherche et de documentation pédagogique, Neuchâtel.