
Banca di problemi del RMT
td128-it
 |
Banca di problemi del RMTtd128-it |
|
Dati due rettangoli omotetici, posizionare l'immagine di un punto dal primo sul secondo.
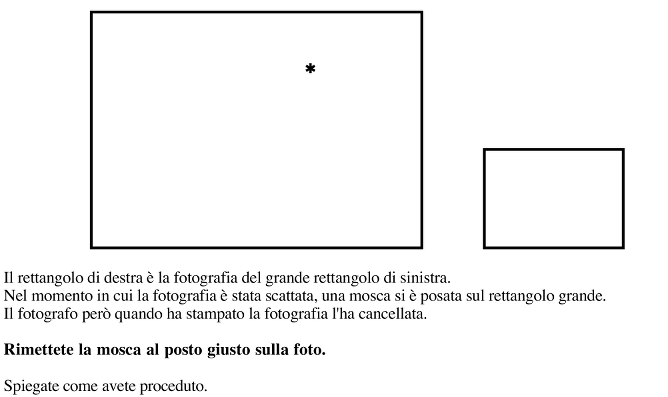
Osservare le due figure e rendersi conto che la trasformazione che passare dall’una all’altra è un’omotetia (o riduzione.
Mettere in opera le conoscenze sulle trasformazioni come:
- determinare il fattore di riduzione della fotografia a partire dai due rettangoli e verificare che è il medesimo per le due dimensioni: 2,5/6 = 3,5/8,4 = 5/12, determinare poi le coordinate della mosca sul foglio e calcolare le coordinate corrispondenti sulla foto;
- o cercare di “quadrettare” i due rettangoli;
- oppure utilizzare una procedura geometrica tracciando due rette passanti ciascuna per la mosca e un vertice del foglio e conducendo poi le parallele corrispondenti sulla foto;
- oppure cercare il centro di omotetia, etc.
omotetia, ingrandimento, riduzione, proporzionalità, parallelismo, coordinate
I punteggi non sono stati conservati, ma un’analisi a posteriori su 234 classi di due sezioni della Svizzera e di quattro sezioni italiane ha consentito di fare le osservazioni riportate nei paragrafi che seguono.
Su 234 classi che hanno affrontato il problema, ci sono state solo 7,7% non risposte, cosa che significa che in generale gli allievi si sono appropriati del problema e hanno affrontato la ricerca della posizione della mosca sulla foto. Le strategie di risoluzione possono essere classificate secondo due grandi categorie: numeriche e geometriche.
1. Le procedure numeriche
Rientrano in questa classe procedimenti che utilizzano il coefficiente di proporzionalità (dato, ad esempio, dal rapporto tra la lunghezza del rettangolo grande e quella del piccolo) e procedimenti che sfruttano la proprietà moltiplicativa di linearità, esprimibile con f(kx)=f(x).
Ciascuna delle due tipologie di soluzioni prevede al proprio interno un’articolazione in sottoclassi.
1.1 Uso del coefficiente di proporzionalità
Nel testo del problema si invita a considerare un «oggetto» e una sua fotografia, esempio classico per introdurre il discorso sulle figure simili.
Negli elaborati di questo raggruppamento si coglie la similitudine dei rettangoli e si individua la chiave per risolvere il problema nel calcolo del coefficiente di proporzionalità tra le due figure e nell’applicarlo alle «coordinate» della mosca nel rettangolo grande.
- In alcuni casi, in particolare in categoria 7 e 8, il coefficiente è determinato considerando una sola dimensione, ovvero una sola coppia di lati corrispondenti nei due rettangoli.
Abbiamo misurato il lato minore del rettangolo grande e di quello piccolo, in seguito abbiamo calcolato il loro rapporto, che è di 2,4. Misurata la distanza della mosca dai due lati, abbiamo diviso per il rapporto le due distanze e abbiamo riportato perciò la mosca nel rettangolo piccolo.
- oppure, il coefficiente di proporzionalità è calcolato due volte, ovvero su entrambe le dimensioni dei rettangoli. Non si sa se tale procedura è vista dagli allievi come una verifica o come una necessità; di sicuro, in alcuni casi essi non sono coscienti che i due calcoli devono dare lo stesso risultato e accettano di ottenere valori diversi, utilizzandoli entrambi per posizionare la mosca.
- o ancora, il rapporto tra le aree ma lo si usa come coefficiente di proporzionalità tra i due rettangoli. Questo procedimento è illustrato nell’elaborato seguente (di livello 7) in cui compare anche un uso appropriato delle «lettere» in luogo dei numeri:
Si è diviso l’area del rettangolo grande per l’area del rettangolo piccolo. Risultato della divisione x. Poi si è misurato a quanti cm si trova la mosca dal bordo a e dal bordo b [sono indicati con a e b due lati consecutivi del rettangolo grande]: prima lunghezza y, seconda lunghezza z. Dopo si è diviso y e z per x che ci dà due nuove lunghezze. Per finire si sono utilizzate queste nuove lunghezze sul rettangolo piccolo per posizionare la mosca che si trova all’intersezione delle due lunghezze.
- in una trentina di elaborati il coefficiente di proporzionalità è determinato approssimativamente e applicato alle lunghezze, in particolare in categoria 6 e stimato come 2.
Qualche volta si è ritenuto che il coefficiente di riduzione fosse 1/3.
Abbiamo trovato la soluzione prendendo le misure giuste e rimpicciolendole di tre.
- solo in elaborati di classi italiane di livello 8, dopo aver notato esplicitamente la similitudine dei due rettangoli, sono state utilizzate le proporzioni per determinare la posizione della mosca sulla fotografia.
Per risolvere questo problema abbiamo usato le proporzioni, applicandole alla similitudine dei due rettangoli. Abbiamo messo in proporzione l’altezza e la larghezza dei rettangoli con la distanza dai lati alla mosca, sia secondo la lunghezza che secondo la larghezza. Abbiamo così trovato la posizione della mosca nel rettangolo più piccolo».
1.2 Uso di un rapporto di linearità
Negli elaborati di questa tipologia di procedure, il procedimento si basa sulla ricerca dei rapporti tra ciascuna delle coordinate della mosca nel rettangolo grande e una delle dimensioni di quest’ultimo e nell’utilizzare tali rapporti per determinare le coordinate della mosca nel rettangolo piccolo. Si trova ad esempio una spiegazione di questo tipo in categoria 7. Per poter posizionare la mosca sul riquadro piccolo, bisogna misurare il lato grande del riquadro grande e guardare dove la mosca si trova in rapporto al lato grande. Poi bisogna riportare il punto alla scala del riquadro piccolo. E ricominciare con il lato piccolo del riquadro grande.
E troviamo:
1.2.1 Procedure corrette per via aritmetica o geometrica
In alcuni elaborati il procedimento è descritto per via aritmetica, dopo aver eseguito le opportune misurazioni. In altri si privilegia, invece, una procedura di tipo geometrico. Ho diviso AB in 3 parti. Ho fatto lo stesso nel rettangolo piccolo. Ho diviso BC in 4 parti: Ho fatto lo stesso nel rettangolo piccolo.
1.2.2 Procedure incomplete o con conclusioni errate
In qualche caso la spiegazione fornita evidenzia che si è lavorato solo su una delle coordinate della mosca e si è tralasciato del tutto l’altra. La posizione della mosca sulla foto si ottiene probabilmente sostituendo il dato mancante con una valutazione «ad occhio».
In un caso, in particolare, sono determinati in modo corretto i rapporti tra le misure delle dimensioni del rettangolo e le coordinate della mosca, ma tali valori sono presi poi per indicare direttamente la posizione della mosca sulla foto.
2. Le procedure geometriche
Le sole procedure puramente geometriche (55 su 234) si hanno in quegli elaborati che presentano costruzioni basate sulla conservazione degli angoli o del parallelismo, sull’omotetia, sulla suddivisione dei rettangoli con rette parallele ai lati o con «diagonali», sulla riproduzione del rettangolo piccolo sopra a quello grande.
2.1 Conservazione degli angoli
Questo tipo di procedimento si è riscontrato solo in elaborati svizzeri.
2.1.1 Riporto di angoli o conservazione per parallelismo dei lati Due esempi significativi, in cui la posizione della mosca è individuata attraverso il riporto di angoli eseguito con riga e compasso, oppure la costruzione geometrica che evidenzia come gli angoli siano mantenuti attraverso la conservazione del parallelismo tra i lati.
2.1.2 Idea intuitiva di conservazione degli angoli attraverso la conservazione di un’inclinazione della retta che passa per la mosca e il punto di intersezione delle diagonali del rettangolo.
In alcuni protocolli, dopo aver disegnato le mediane nel rettangolo grande, si traccia la semiretta che congiunge il loro punto di incontro con il punto in cui si trova la mosca e si ripete la costruzione sull'altro rettangolo, in modo che le semirette abbiano uguale inclinazione.
2.2 Uso dell’omotetia e del teorema di Talete
In due elaborati svizzeri di livello 7 ed in uno italiano di livello 8, la posizione della mosca nella fotografia si ottiene attraverso una costruzione che evidenzia come i due rettangoli siano corrispondenti l’uno dell’altro in una omotetia. Una bella costruzione riportata mette in evidenza (anche se con qualche imprecisione formale) il centro di omotetia, il rapporto di omotetia (12/5) e la conservazione delle proporzioni tra segmenti attraverso il parallelismo (teorema di Talete).
2.3 Metodo per approssimazioni successive
Negli elaborati in cui si applica questo tipo di procedura, la posizione della mosca viene determinata, in modo approssimato, restringendo via via la zona della sua localizzazione con opportune suddivisioni del rettangolo grande, riportate poi sull’altro (è presente l’idea di conservazione della forma in quanto tutto ciò che si disegna sul rettangolo grande è riprodotto nello stesso modo sul piccolo, non si fa però riferimento alla similitudine e alle sue proprietà).
2.3.1 Con triangolazioni
Abbiamo individuato un modo per sapere dove è esattamente la mosca nel rettangolo e abbiamo riprodotto il disegno.
le spiegazioni fornite sono molto sintetiche e lasciano pensare che la posizione della mosca, una volta circoscritta la parte del rettangolo in cui essa si dovrebbe trovare, sia individuata «ad occhio» o al più tenendo conto di una sola misura (per esempio la distanza della mosca da una diagonale del rettangolo grande) riportata senza riduzione nel rettangolo piccolo.
2.3.2 Con quadrettatura
La quadrettatura dei due rettangoli è realizzata direttamente sulle figure di partenza o riproducendo le stesse su carta a quadretti. I quadretti possono essere «uguali» nei due rettangoli, e allora il fattore di scala viene espresso in termini di un quadretto del rettangolo piccolo corrisponde ad n quadretti del rettangolo grande, oppure sono presi in scala.
2.4 Rettangolo piccolo considerato come porzione del grande
In questi elaborati manca del tutto l’idea di similitudine: la posizione della mosca è determinata considerando il rettangolo piccolo come porzione del grande.
2.4.1 Per sovrapposizione
È la procedura più usata e consiste nel riportare (con il disegno o per ritaglio e sovrapposizione) il rettangolo piccolo sul grande facendone combaciare i vertici in alto a destra e «ricalcando» poi sul rettangolo piccolo la posizione della mosca.
Con il procedimento descritto, però, il punto in cui viene situata la mosca nel rettangolo piccolo risulta in netto contrasto con una sua individuazione «ad occhio» (la mosca si viene a trovare in basso a sinistra).
In alcuni elaborati gli allievi si rendono conto di questa anomalia e, per avere un risultato «compatibile» con l’intuizione, effettuano una rotazione del rettangolo corrispondente alla foto.
In un elaborato è invece evidente che gli allievi hanno "giustificato” senza difficoltà la posizione "anomala" della mosca perché non hanno considerato i due rettangoli ugualmente "orientati" (fatto ritenuto ovvio nel testo e quindi non dichiarato): Essendo il negativo posizionato al contrario rispetto all’immagine della foto, la mosca si troverà nella parte opposta rispetto al rettangolo principale.
2.4.2 Per ricoprimento
Si «pavimenta» il rettangolo grande con rettangoli congruenti a quello piccolo in modo che uno di essi contenga la mosca, se ne riproduce su questo la posizione e si riporta poi il punto trovato sulla foto. In qualche caso si ritrova ancora la necessità di giustificare la posizione della mosca con una rotazione del rettangolo piccolo Si misura la larghezza e la lunghezza della mosca sul riquadro grande, poi si riporta sul riquadro piccolo. Si gira il riquadro al contrario e questo ci fa la mosca.
Une trentina di elaborati, in particolare di categoria 6 e talvolta 7, non danno alcuna indicazione circa la maniera con la quale è stata sistemata la mosca o danno solo qualche cenno di spiegazione.
Infine qualche raro elaborato indica che c’è stata un’incomprensione totale del problema.
Doretti.L. Dorsaz. M. Peix. A. Rinaldi. M-G. Strategie usate nella risoluzione di un problema sulla similitudine / Stratégies utilisées dans la résolution d'un problème de similitude. RMT: evoluzione delle conoscenze e valutazione dei saperi matematici RMT : évolution des connaissances et évaluation des savoirs mathématiques Ed. Grugnetti & al. Università di Siena, IRDP Neuchâtel 2000.
© ARMT, 1999-2022
(c) ARMT, 1999-2024