
Banque de problèmes du RMT
ud13-fr
 |
Banque de problèmes du RMTud13-fr |
|
Déterminer l'aire d'une figure délimitée par des arcs de cercle (serpent) inscrite sur un quadrillage.
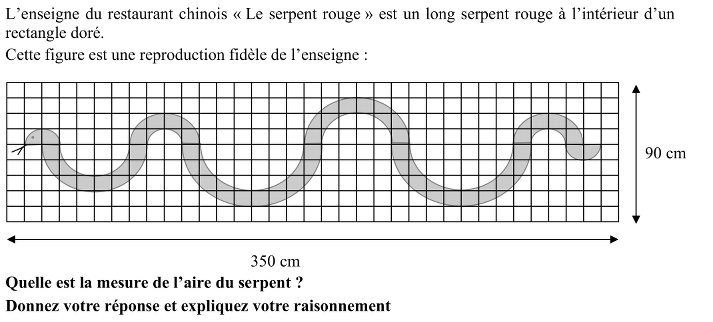
Analyse a priori:
- Comprendre, à l’analyse de la figure que le corps du serpent est formé de deux demi-disques équivalents (tête et queue) et de six demi-couronnes circulaires, équivalentes deux à deux, et que le côté d’un carré du quadrillage mesure 10 cm.
- Observer que, en assemblant les couronnes et les demi-disques, on obtient un seul disque de 40 cm de rayon.
Ou :
- Procéder par le calcul des aires des couronnes circulaires (la plus grande de 40 cm de rayon externe et 30 cm de rayon interne, la moyenne de 30 cm de rayon externe et 20 cm de rayon interne, la petite de 20 cm de rayon externe et 10 cm de rayon interne) et des demi-disques (de 10 cm de rayon).
- Conclure, dans les deux cas, que l'aire demandée est 1600 π, en cm2
aire, cercle, disque
Les résultats n'ont pas été conservés ou ne sont pas encore disponibles.
(c) ARMT, 2004-2024