Tapis carrés

Identification

Rallye: 09.II.14 ; catégories: 7, 8 ; domaines: FN, AL, GM
Familles:

• MEQ - Etablir puis résoudre des (in)équations
• MEQ/EQ2 - Résoudre une équation du 2e degré
• RD - Rechercher ou utiliser des dimensions

Remarque et suggestion

Résumé

Etablir les relations entre la mesure du côté d'un quadrillage carré n x n, son aire et le nombre de “chaînettes” dessinées sur son pourtour (2 par côté de carreau, 1 à chaque sommet du carré et à chaque sommet commun des carreaux. Chercher ensuite si l’on peut trouver un quadrillage dont le nombre de carreaux est le même que le nombre de chaînettes et un quadrillage dont le nombre de carreaux vaut 40 de plus que le nombre de chaînettes.

Enoncé

Tâche de résolution et savoirs mobilisés

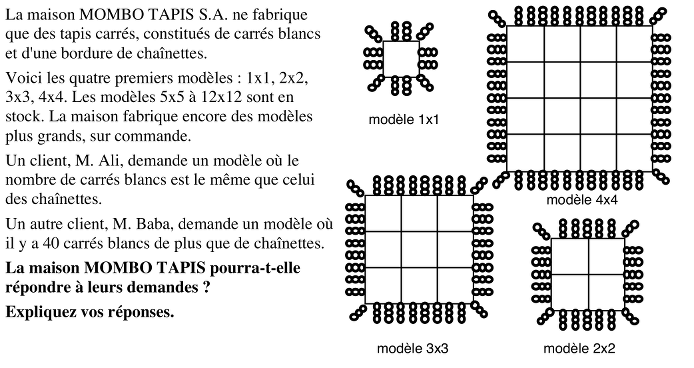
- Trouver les nombres de carrés et de chaînettes des premiers tapis et leur expression générale (avec ou sans lettres):

  numéro       1   2   3   4   5  ...	n
  carrés       4   9  16  25  36  ...	nxn ou n^2, ou le "nombre élevé au carré"
  chaînettes  12  24  36  48  60  ...	nx12 ou 12n

- Continuer, pour M. Ali, les suites jusqu'à 12 et 144 ou résoudre l'équation 12n = n² et en déduire que la demande pourra être honorée, pour le modèle 12x12.

- Poursuivre, pour M. Baba, la suite au-delà de 12 : 13 -->169 et 156, 14 -->196 et 168, 15 -->225 et 180 pour constater qu'on ne trouve pas une différence de 40, ou résoudre l'équation n² - 12n = 40 et voir que ses solutions ne sont pas des nombres entiers.

Résultats

Les résultats n'ont pas été conservés ou ne sont pas encore disponibles.

Bibliographie

Voir aussi Le retour de Mombo Tapie (19.I.16)

(c) ARMT, 2001-2025