
Banque de problèmes du RMT
ud189-fr
 |
Banque de problèmes du RMTud189-fr |
|
Etant donné deux types de spirales: l'une "rectangulaire", formée de segments successifs, l’autre, circulaire, formée de demi-cercles successifs, déterminer le nombre minimum de segments nécessaires pour former une spirale rectangulaire plus longue qu’une spirale circulaire formée de 30 demi circonférences.
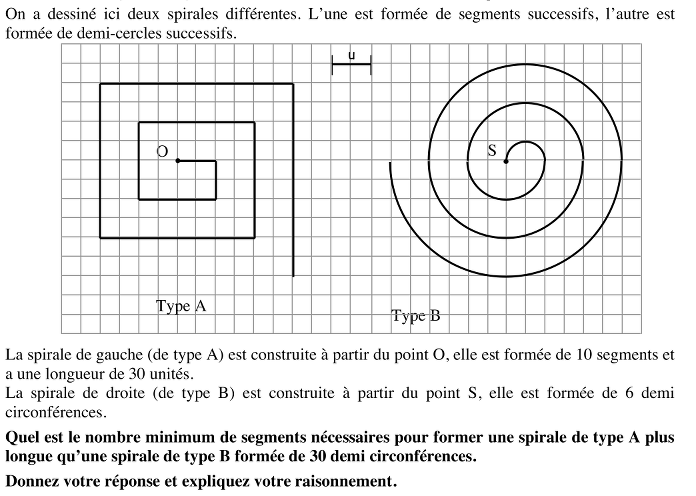
- Comprendre les règles de construction des spirales et voir comment les poursuivre par adjonctions de segments ou de demi circonférences.
- Comprendre qu’il s’agit de déterminer les longueurs des spirales des deux types et que ces mesures dépendent du nombre de segments et de demi circonférences (sont fonction de ce nombre). - Calculer les longueurs de la spirale de type A en observant les premiers segments dessinés et les noter de manière organisée (comme par exemple dans le tableau ci-dessous).

et chercher à trouver des liens entre les nombres des deux suites, selon leur parité par exemple.
- Découvrir que, si le nombre des segments est impair (en désignant par 2n+1 le nombre de segments), la longueur totale, en unités u, est le carré de la moitié du « nombre de segments + 0,5 » (ou (n+1)2 en notation algébrique)alors que, pour les nombres pairs de segments, la longueur totale est le produit de la moitié du nombre de segments par « un de plus que cette moitié » (ou n(n+1) en notation algébrique).

Ou, par voie arithmétique, si le nombre de segments est pair, la longueur des spirales successives s’obtient par la somme suivante :
1+1+2+2+3+3+…+n+n = 2(1+2+3+…+n) = 2 n(n+1)/2 = n(n+1);
si, le nombre est impair, c’est-à-dire de la forme 2n+1, on a:
1+1+2+2+3+3+…+n+n+(n+1) = 2 n(n+1)/2 + (n+1) = n(n+1)+(n+1)= (n+1)2.
- Calculer les longueurs de la spirale de type B en observant les premières demi circonférences et constater que leurs rayons augmentent régulièrement :
1/2 u, 1u, 3/2 u, 2 u,… , (n/2) u, … .
En déduire qu’une spirale de type B, constituée de n demi circonférences a une longueur de:
π/2 + π + (3/2)π + 2π + … + (n/2)π = π/2(1+2+3+…+n) = (π/2)[n(n+1)/2]= (π/4)[n(n+1)].
et éventuellement arriver à la formula LB(n) = (π/2)[n (n+1) / 2] = (π/4)[ n(n+1)].
- Trouver que la longueur d’une spirale de 30 demi circonférences est, en unité u :
LB(30) = (1 + 2 + 3 +…+ 30) π /2 = 232,5 π
et éventuellement en utilisant la formule (π/4)×30×31= 232,5π); en considérant que 3,14 < π < 3,15, on obtient
730,05 < LB(30) < 732,375.
- Comprendre qu’il faut trouver une spirale de type A dont la longueur est supérieure à 733 puis revenir à son nombre de segments.
- À partir, par exemple, des carrés des nombres impairs, constater que le plus proche de 733 est 272 = (n+1)2 = 729 (et que 292 = 841), correspondant à une spirale de type A de 2n+1 = 2×26 + 1= 53 segments. Donc il faut passer à la spirale de type A de 54 = 2n segments et vérifier que sa longueur est 27×28 (= n(n+1)) = 756 (> 732,375).
- Conclure que la spirale de type A recherchée est celle de 54 segments.
régularité, séquence, somme, approximation, spirale
Les résultats n'ont pas été conservés ou ne sont pas encore disponibles.
(c) ARMT, 2010-2024