
Banque de problèmes du RMT
ud193-fr
 |
Banque de problèmes du RMTud193-fr |
|
Envoyer une remarque ou une suggestion
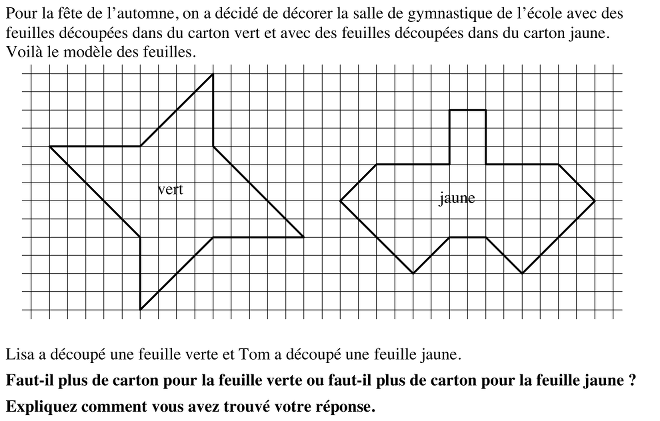
Comparer les aires de deux polygones (de 8 et 12 côtés) dessinés sur un quadrillage, dont les sommets sont sur des intersections du quadrillage et dont les côtés suivent les côtés ou les diagonales des carreaux du quadrillage, dans un contexte de feuilles à découper.
Analyse de la tâche a posteriori
Appropriation de la situation
La lecture de l'énoncé doit faire apparaître les deux objets: feuille découpée dans du carton vert et feuille découpée dans du carton jaune qui sont représentées sur un quadrillage, avec leurs formes et leurs positions ; ce qui va permettre de les comparer selon la quantité de "carton utilisé".
Avant d'entrer dans la résolution, il faut comprendre que la grandeur "carton utilisé" se rapporte à la "place ou à l'espace occupé" par l'objet ou par la partie à colorier en vert ou en jaune, ou à ce qu'on désigne par "surface" ou par "aire" des deux objets découpés ou de leurs dessins.
Un premier débat au sein du groupe devrait permettre de rejeter l'idée de s'intéresser à la longueur du pourtour de chaque dessin (une suite de segments qui détermine un espace fermé) et à porter l'attention sur cet espace intérieur.
Savoirs mobilisés
Vu la présence du quadrillage sur lequel les feuilles ont été dessinées (ce ne sont pas les objets "feuilles" qui sont quadrillées), il suffit de savoir compter les carreaux entiers puis de savoir que deux demi-carreaux (triangles isocèles rectangles situés sur les bords de chaque dessin) forment un carreau entier, qu'on pourra ajouter aux précédents. C'est le concept d'unité d'aire qui est en jeu derrière le quadrillage et le rapport 1 à 2 ou 2 à 1 entre les unités "triangle" et "carré".
En unité "carré" ou "carreau entier", on trouve 61 (52 entiers et 18 triangles) pour la figure verte et 62 (54 entiers et 16 triangles) pour la jaune. (En unité "triangle" les réponses seraient 122 et 124, mais le contexte, avec une majorité de carreaux entiers, ne favorise pas ces réponses, qui exigent la maîtrise du rapport 2 à 1).
(Au cas où ce sont les « morceaux » qui sont comptés, sans tenir compte de leurs aires respectives, on obtiendrait 70 pièces pour la figure verte et 70 pour la jaune. Ce qui signifie que la concept d'unité d'aire n'est pas encore construit.)
Une procédure qui permet d'éviter les éventuelles erreurs de comptage un à consiste à décomposer les figures en rectangles, carrés et triangles et se rendre compte que les triangles observés sont des moitiés de carrés. Il faut savoir ici passer à l'arithmétique par les additions répétées ou multiplications permettant de "calculer" les aires de rectangles et/ou carrés.
En cas de d'hésitation entre aire et périmètre, certains groupes peuvent mesurer les longueurs de leurs côtés, ou compter les côtés ou diagonales de carreaux qui constituent le périmètre, avec l'obstacle de deux unités de longueur différentes, ce qui conduirait à dire que la figure verte est plus grande. De même une confusion entre aire et « encombrement » (plus grande longueur intérieure, par exemple entre deux sommets de la figure) conduirait au même résultat.
sur 1352 classes de 21 sections
| Catégorie | 0 | 1 | 2 | 3 | 4 | Nb. de classes | Moyenne |
|---|---|---|---|---|---|---|---|
| Cat 3 | 148 (47%) | 60 (19%) | 32 (10%) | 34 (11%) | 44 (14%) | 318 | 1.26 |
| Cat 4 | 148 (30%) | 60 (12%) | 57 (12%) | 93 (19%) | 131 (27%) | 489 | 2 |
| Cat 5 | 119 (22%) | 50 (9%) | 74 (14%) | 105 (19%) | 197 (36%) | 545 | 2.39 |
| Total | 415 (31%) | 170 (13%) | 163 (12%) | 232 (17%) | 372 (28%) | 1352 | 1.98 |
| Rappel: Le problème est résolu dans les conditions particulières du RMT: classe entière, élèves en autonomie complète, 5 à 7 problèmes à résoudre, une seule feuille de réponses par problème. | |||||||
Selon les critères déterminés lors de l’analyse a priori :
Une première analyse a posteriori, partielle, a alimenté l'article de Lucia Grugnetti: "Analyse a priori, analyse a posteriori, au delà de la démarche circulaire" publié dans la Gazette de Transalpie no 4, août 2015, pp. 75-94. dont voici quelques extraits:
… Comme on le voit dans la rubrique attribution des points, le « 0 point » envisage le recours au périmètre pour comparer les figure ou au comptage des pièces sans tenir compte de leur aire.
-L’analyse effectuée par les membres du groupe géométrie, au sein de leurs sections d’appartenance, et largement décrite dans Anselmo et al. (2011), montre que, en effet, le « 0 point » est toujours attribué pour l’une des deux difficultés signalées et non par « incompréhension du problème ». Et, pour cette attribution, les pourcentages décroissent en passant de la catégorie 3, (49%, sur 290 copies) à la 4 (30%, sur 489 copies) et enfin à la 5 (22% sur 545 copies).
- Ces résultats indiquent de toute manière que, en catégorie 5, les élèves rencontrent les difficulté et obstacles cités précédemment, même si sont moins fréquents. Il sera important de proposer d’autres problèmes similaires afin de vérifier encore l’existence de ces difficultés mais aussi pour chercher à comprendre à quel âge elles sont surmontées.
- Le parcours qui va de l’analyse a priori à l’analyse posteriori, pour retourner à l’analyse a priori, de circulaire à l’origine prend en quelque sorte une forme en spirale : une spirale de parcours circulaires successifs. Dans ce cadre, l’attention est centrée sur les difficultés et les obstacles, mais il est important de se rappeler que les analyses a posteriori des problèmes du RMT prennent en considération toute la gamme des réponses et des explications ; il arrive souvent qu’on se rende compte du nombre important de types de solutions prospectées par les élèves et auxquelles les adultes n’avaient pas pensé lors de la préparation de l’analyse de la tâche.
//En voici un bel exemple ://
Exemple 1

Analyse a posteriori en vue de l'exploitation du problème en classe. (2025)
L'examen des copies d'un échantillon de 142 copies de la section de SI fait apparaître :
a) 20% : réponses 62 (jaune) 61 (verte), comptage détaillé, (ou erreur de comptage) ou parfois décomposition et recomposition des figures en triangles, rectangles et carrés, ou comparaison par découpage et superposition (comme dans l'exemple 1 précédent.
Exemple 2 (cat 5)
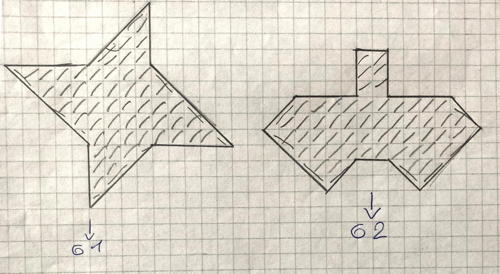
Il y a bien 61 et 62 traits sur ces figures, certains plus longs que d'autres car ils recouvrent deux triangles qui sont comptés comme 1 trait ou carreau entier, avec maîtrise du rapport 2 pour 1.
b) 15% : réponses ("jaune" le plus souvent) sans autre explication que "nous avons compté les carreaux".
c) 10% : réponse 70 (jaune) 70 (verte), (ou erreur de comptage) correspondant au nombre total de carreaux entiers et de triangoli (demi carrés).
d) 20% : réponses entre 30 et 36 correspondant au comptage des carreaux disposés sur le périmètre ou, des côtés et diagonales des carreaux du périmètre.
Exemple 3 (cat 4)
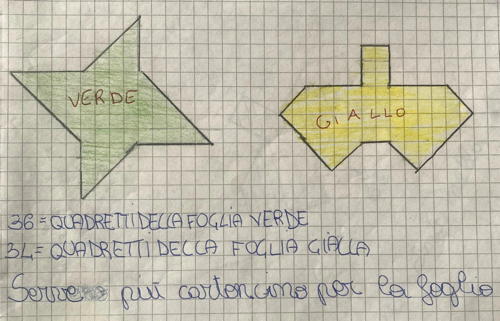
Nous avons compté le contour des deux feuilles. Au début on a trouvé qu'ils étaient égaux mais en comptant mieux nous avons compris que la feuille verte avait besoin de 36 carreaux et le jaune de 34.)
e) 35% : autres réponses comme "incompréhension du problème" ou mesures en cm et application incorrecte des formules d'aire, ou erreur de dessin.
Exemple 4 (cat 5)
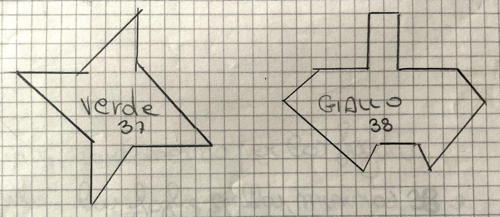
Exemple 5 (cat 4)
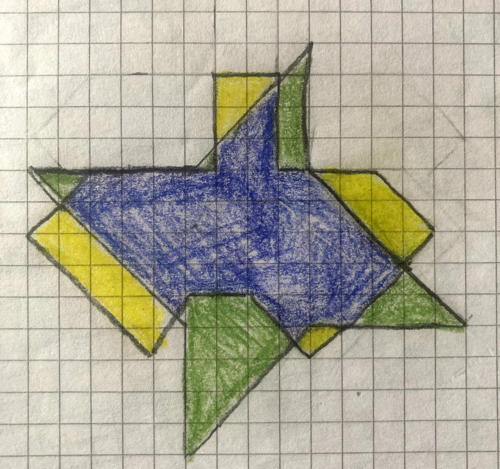
Ces élèves ne maîtrisent pas le report d'un dessin sur quadrillage, comme ceux de l'exemple suivant qui, travaillent par "superposition"
Ce sont ces types de réponses que l'enseignant verra probablement apparaître lors de la mise en commun des résultats.
la phase la plus délicate pour l'enseignant est de gérer la discussion collective des résultats sans vouloir "enseigner" parce que la parole est aux élèves, qui doivent se rendre compte que les réponses 61 et 62 sont correctes, qu'on peut les justifier par le comptage un à un ou par décomposition puis recomposition ou par superposition”. Ils doivent aussi pouvoir justifier le rejet des réponses de type c, (avec additions d'unités différentes) de type d, (confusion aire et périmètre) ou autres erreurs.
L'enseignant doit observer, poser des questions pour faire expliciter les arguments des élèves. Chaque détail peut être pris en considération en fonction des avoirs à renforcer (voir rubrique précédente sur les Savoirs mobilisés).
À propos de l'exemple 3 précédent, des feuilles coloriées, demander ce que signifie le mot "contour", puis de montrer d'où viennent les 34 et 36 "carreaux" pour faire constater qu'il s'agit de 34 et 36 "côtés" ou "diagonales" de carreaux, puis demander encore aux auteurs de cette copie si ces "côtés" et "diagonales" sont de même longueur.
À la fin de la mise en commun, il s'agit d'organiser le travail individuel pour que chaque élève tire profit de ce qui a été dit collectivement car, évidemment les réponses 61 et 62, bien justifiées sont loin d'être suffisantes du point de vue des savoirs à reconstruire ou à renforcer.
Voci un programme minimum pour la phase "d'étude individuelle" qui devrait figurer dans le cahier de chaque élève :
1. dessiner les deux feuilles sur papier quadrillé et les colorier (aire, dessin sur quadrillage)
2. décrire les deux figures (polygones, nombre de côtés et sommets, …)
3. déterminer laquelle des deux figures a le plus long périmètre (mesure de longueur, unité commune, reports, approximations ...)
4. déterminer l'aire de chacune, en carreaux du quadrillage, en demi-carreaux triangulaires, éventuellement en cm$^2$ dans le cas d'un quadrillage dont les carreaux ont 5 mm de côté (mesure d'aire, unité commune, rapport entre unités communes )
5. si possible, passage à une démarche plus élaborée qui va au delà du comptage un à un, par exemple la décomposition en triangles puis recomposition en carrés (entrée en arithmétique, utilisation de la multiplication ou additions répétées, décomposition et recomposition "additives" de figures géométriques.
Exemple 6 (cat 4)
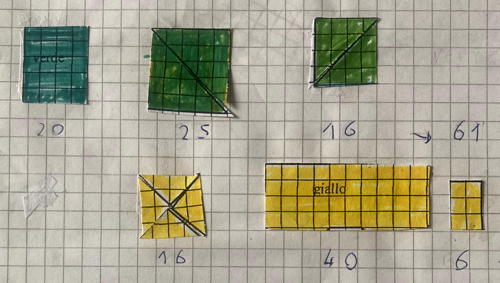
Les écritures 20, 25, 16 -> 61 et 16, 40, 6 -> 62 (tronqué sur la reproduction) montrent que les élèves sont allés au-delà du comptage un à un pour entrer en arithmétique après avoir décomposé les feuilles pour les recomposer en rectangles.
Exemples d'activités en vue d'un parcours didactique avec la classe
À expérimenter en classe, selon des modalités déterminées par l'enseignant; avec envoi de description et commentaires pour rendre compte de l'opportunité de l'activité pour la construction des savoirs (notés en italique).
a) Exprimer les propriétés de symétrie des deux figures (et d'autres) par découpages, pliages, rotations.
La feuille jaune a un axe de symétrie, la feuille verte a un centre de symétrie ou centre de rotation d'un demi-tour, ...).
b) Aligner les côtés des périmètres des deux feuilles en les dessinant à la suite et en distinguant les côtés sur les lignes du quadrillage des segments en oblique;
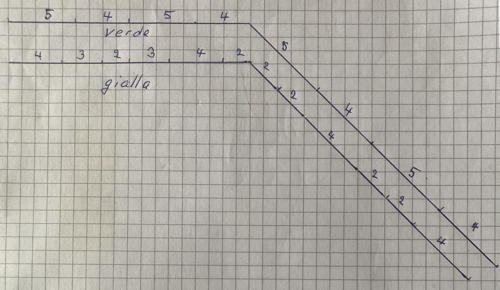
puis à l'aide du compas, reporter les parties "obliques" sur les lignes du quadrillage pour obtenir les deux "périmètres" de longueurs visiblement différentes.
Se rendre compte que les diagonales de carreaux du quadrillage sont plus longues que les côtés de carreaux
c) Rechercher d'autres polygones de 62 carreaux (sur quadrillage avec carreaux entiers ou demi-carreaux, dont celui qui a le périmètre le plus court, et le plus long !!
Se rendre compte qu'il y a beaucoup de polygones de même aire (62 carreaux) et que leurs périmètres peuvent être très différents.
Autres détails et propositions dans l'article Problemi, che passione! en bibliographie.
d) De nombreux autres problèmes traitent des comparaisons d'aires, sur quadrillages, sur réseaux ou par d'autres décompositions en unités d'aires:
La rosace de Julie I (15.II.04), La rosace de Julie II (15.II.07)
Rectangles de papier quadrillé (I) (ral. 29.I.04) Rectangles de papier quadrillé (II) (ral. 29.I.08)
Comparaison de figures (26.I.12)
Le jardin de M. Tordu (08.I.06)
Grugnetti, Lucia (2015). **Analyse a priori, analyse a posteriori, au delà de la démarche circulaire**. Gazette de Transalpie no 4, août 2015, pp. 75-94
Anselmo, Bernard. Bisso, Clara, Grugnetti, Lucia (A nome del Gruppo geometria piana: Bernard Anselmo, Chiara Badiali, Silvana Bisogni, Clara Bisso, Jean-Louis Billody, Fabio Brunelli, Florence Falguères, Lucia Grugnetti, Elisabetta Mari, André Nguyen, Letizia Pucci, Michele Rapuano, Elsa Renna, Samia Mehaddene, M. Francesca Tanda, Agnese Tomasini, Donata Tardio, con la collaborazione di Anna Maria D’Andrea e Francesca Ricci). **Il rettangolo ... non così evidente**. In Gazette de Transalpie no 1, 2011, pp. 7-11
Grugnetti, L. Jaquet, F. Problemi, che passione! (Lugo 14 maggio 2025) In Gazzetta della BPrmt à paraître.