
Banque de problèmes du RMT
ud237-fr
 |
Banque de problèmes du RMTud237-fr |
|
Envoyer une remarque ou une suggestion
Comparer l'aire de deux parties d'un carré.
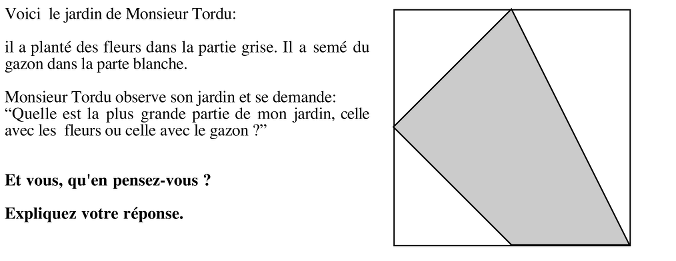
- Imaginer que la partie grise et la blanche se décomposent en mêmes “pièces”
- Vérifier en découpant les “pièces”
- Déduire que la partie des fleurs a la même aire que le gazon
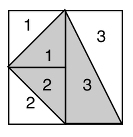
figure, comparaison, aires
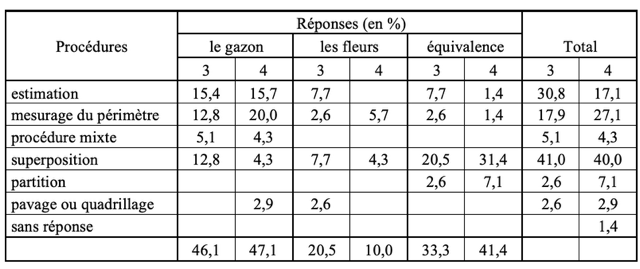
Il n'y a pas de résultats "statistiques" pour ce problème des premières années du Rallye Mathématique Transalpin, Mais une analyse détaillée des réponses d'une centaine de classes, résumés dans la rubrique suivante "Procédures, obstacles et erreurs relevés" et dans l'article "Conflit aire-périmètre" signalé en bibliographie.
Les résultats présentés ici sont ceux des classes des régions de Parma et de Suisse romande : 39 classes de catégorie 3 (respectivement 8 et 31) et 70 classes de catégorie 4 (14 et 56).
Le tableau qui suit présente les différentes procédures relevées (première colonne) :
- "estimation", la réponse se fonde sur une estimation visuelle globale ou mentionne une juxtaposition, un découpage ou une superposition, sans autre précision;
- "mesurage du périmètre", effectué à la règle, avec le détail des calculs ou des périmètres obtenus;
- "mixte", prise en compte simultanée d'éléments caractéristiques de l'aire et du périmètre;
- "superposition", par découpage des trois parties blanches et collage sur la partie grise ou avec détail du recouvrement;
- "partition", procédure prévue par l'analyse a priori (voir figure de la rubrique "Tâche de résolution et savoirs mobilisés"):la partie grise est partagée en trois parties, chacune étant équivalente à l'un des triangles blancs;
Estimation
Dans cette catégorie de procédure, on trouve les réponses fondées sur une estimation visuelle globale ou qui évoquent des comparaisons par déplacements de figures, mais sans aucune trace écrite. Les types d'explications sont assez hétérogènes. Ils vont de "auto conviction" (Ex. 1) à des arguments se référant aux bords des terrains (Ex. 2) ou à des additions de triangles (Ex 3). Dans ce type de réponse, le fait que le gazon soit en trois parties contre une seule pour les fleurs a certainement dû influencer les avis des groupes d'élèves, dont 17 sur 24 choisissent la première possibilité, 3 pensent que ce sont les fleurs et 4 optent pour l'équivalence.
Exemple 1: Nous pensons que la partie en gazon est la plus grande et celle des fleurs la plus petite parce que celle des fleurs est plus petite et celle du gazon est la plus grande du jardin.
Exemple 2: Le champ de fleurs a l'air plus grand mais le plus grand c'est le gazon parce qu'il a des bords plus grands.
Exemple 3: Nous pensons qu'il y a plus de gazon et moins de jardin. Le triangle petit et entier plus un triangle petit et entier forment un carré. Un carré plus un grand triangle à moitié forment une forme d'un carré plus un grand triangle à moitié.
(Les trois triangles "petit et entier" et "grand à moitié" sont désignés explicitement sur le dessin de l'énoncé.)
Mesurage du périmètre
Les groupes qui ont choisi de mesurer tous les côtés des différentes parties du jardin pour les comparer devaient logiquement arriver à la conclusion que le gazon est le plus grand. Mais on ne compte que 19 réponses "gazon" parmi les 26 classes qui ont opté pour cette procédure; il y a aussi 5 réponses "fleurs" et 2 réponses "équivalence".
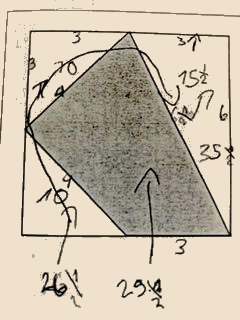
Exemple 4 La plus grande partie du jardin de M. Tordu est la partie grise. Pour trouver la réponse nous avons calculé avec une règle. Et, nous avons additionné les nombres. La réponse est 29 1/2.
(Première confusion entre les mesures "4" de deux côtés du quadrilatère et les périmètres "10" notés dans les triangles de gauche : 10 + 10 + 3 + 6 1/2 = 29 1/2. Seconde confusion pour la partie blanche : 10 + 10 + 6 1/2 = 26 1/2 à la place de 10 + 10 + 15 1/2 = 35 1/2, pourtant noté.
Procédure mixte
Il y a peu de réponses appartenant à cette catégorie de procédures, mais elles paraissent révélatrices d'un changement de représentations par rapport à celles de la catégorie précédente reposant sur des mesures de côtés et sur leur addition systématique.
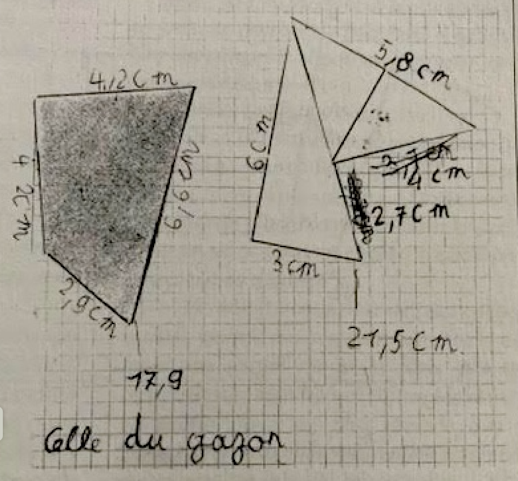
Exemple 5 Une classe a découpé les trois triangles de gazon pour les réassembler en un seul polygone, un quadrilatère comme la partie des fleurs, mais convexe. Elle a ensuite calculé les deux périmètres, correctement, pour trouver 17,9 et 21,5 cm. L'idée de conservation de l'aire dans l'assemblage des trois triangles est clairement sous-entendue, l'accent sur le périmètre n'est donné qu'au moment de la comparaison numérique. Il n'y a plus, comme précédemment, une addition systématique des périmètres de toutes les parties. Les côtés communs des triangles assemblés ne sont plus pris en compte.
Superposition
La procédure par "superposition" est de loin la plus fréquente, tant en catégorie 3 qu'en catégorie 4, choisie par 40 % des classes dans chacun des degrés. C'est aussi la plus efficace, après la procédure par "partition" : sur les 44 classes qui ont superposé les parties, 30 ont conclu à leur équivalence (68 %). La réussite est plus forte en quatrième année (22 sur 28 ou 79%) qu'en troisième année (8 sur 16 ou 50%).
Il y a cependant des réponses erronées par superpositions qui semblent correctes:
Exemple 6 La partie grise est plus grande que la blanche, nous le prouvons avec ces pièces. Voici le résultat.
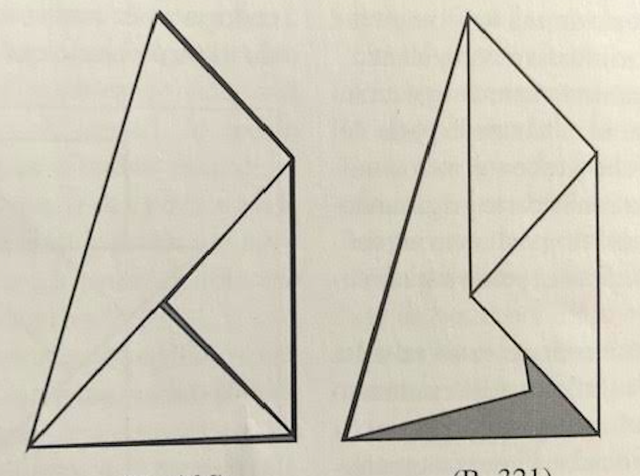
Le recouvrement par collage semble parfait mais le commentaire le dément, en raison de petits filets gris qui apparaissent sous les trois triangles blancs (voir partie gauche de la figure suivante).
Exemple 7 On a découpé le gazon et on a recouvert les fleurs et on a constaté qu'il y avait plus de fleurs que de gazon.
Le recouvrement n'est pas parfait, les élèves ne remarquent pas que dans le rabattement du grand triangle rectangle, il n'y a pas superposition du petit côté de l'angle droit sur le côté du quadrilatère et qu'il y a des superpositions (voir partie droite de la figure suivante.)
Une remarque générale s'impose à propos de cette catégorie de procédures "par superposition" : aucun des groupes n'a accompagné ses manipulations d'argumentations. Que l'équivalence des deux parties ait été reconnue ou non, les explications fournies ne reposent que sur les découpages, superpositions ou collages d'objets réels : formes blanches et grises, parties de gazon, pièces, gazon, fleurs, ... . Les conclusions s'expriment aussi en termes de grandeurs physiques ou de manipulations: on arrive à la même forme, les deux parties sont la même chose, c'est la même grandeur, parties égales, on arrive à les placer, on a vu que l'herbe est plus grande, ... .
Partition
La différence entre les réponses de cette catégorie et celle de la précédente ne sont pas évidentes en première analyse car les élèves de ces groupes ont aussi découpé les différentes parties. C'est au moment de la justification qu'apparaissent les éléments caractéristiques de ces explications : une partition du quadrilatère en trois zones explicitement comparées aux trois parties de gazon. Les dessins sont proches de ceux de la catégorie précédente où figure le carré d'origine (exemple de droite dans la figure précédente), mais les trois partie ne sont plus de simples collages, il s'agit plutôt de la transcription d'une image mentale où le carré initial n'est pas dessiné par commodité ou par hasard mais pour faire apparaître la répartition en six parties, équivalentes deux à deux.
On trouvera ne nombreux autres exemples de ces procédures dans l'article Il conflitto area-perimetro / Le conflit aire-périmètre mentionné en bibliographie.
Ce problème a été choisi comme exemple de L’importance des problèmes du Rallye mathématique transalpin dans la pratique de classe, objet d'un travail pratique de longue haleine présenté lors de la réunion internationale de l'ARMT à Faenza en 2023. (Voir blbliographie).
A la lecture de cet exemple, on comprend que l'activité doit se dérouler dans une ambiance de recherche libre et active, avec manipulations (mesures, découpages, collages, ...), confrontations et échanges.
Les données issues de l'analyse précédentes sont suffisantes pour comprendre la richesse potentielle de la reprise du problème en classe, pour donner du sens à la mesure de longueurs et à l'approche du concept d'aire.
Exemples d'activités en vue d'un parcours didactique avec la classe
À expérimenter en classe, avec envoi de commentaires pour rendre compte de son opportunité pour l'apprentissage.
1. Découpage des quatre pièces, reconstitution du carré et /ou superposition de la plus grande pièce par les trois autres
Observations: ce "puzzle" de quatre pièces plaît beaucoup aux élèves, dont certains mémorisent plus facilement que d'autres les modalités de reconstruction du carré d'origine, même si les pièces sont retournées et toutes blanches, sans distinguer a priori la pièce grise. Derrière cette activité d'ordre tactile, il peut y avoir cependant une progression dans la nature des "savoirs" en jeu: la reconnaissance des quatre formes (deux petits triangles isocèles rectangles ou "demi-carrés", un triangle rectangle non isocèle, un quadrilatère. Il y a quatre longueurs de côtés en présence: la plus petite se retrouve dans chacune des quatre formes (deux fois dans les petits triangles et une fois dans les deux autres; la suivante est l'hypoténuse des petits triangles qui se retrouve deux fois dans la quadrilatère; la troisième est la longueur du carré d'origine qui est un des côtés de l'angle droit du triangle non isocèle; la quatrième longueur est celle du côté commun au triangle non isocèle (son hypoténuse) et au quadrilatère (son côté le plus long). Ce sont ces relations entre ces quatre longueurs qui déterminent les modalités de reconstruction du carré d'origine ou de la superposition du quadrilatère. Si l'élève ne les prend pas en compte, la reconstruction du carré ne peut se faire que pat essais répétés puis par mémorisation de son "algorithme"; si l'élève en est conscient, la reconstruction est simplifiée et s'insère dans un parcours déductif. (Par exemple, les deux côtés les plus longs seront juxtaposés de deux manières seulement.)
D'autres relations peuvent se révéler utiles: chaque forme a un angle droit; la plus petite longueur est la moitié de celle du côté du carré; il y a des rapports entre les aires des triangle et celle du carré d'origine; ... . Ainsi, la "simple" activité de "puzzle" peut participer au renforcement de connaissances sur les longueurs, aires et angles de ces pièces; l'enseignant peut en profiter pour les expliciter.
2. Dessin de la figure d'origine sur papier quadrillé, avant le découpage ou sans découpage
// L'activité précédente "puzzle" ne met pas en évidence l'unité commune "aire du petit triangle" pour exprimer les mesure des aires du carré d'origine (8) et des quatre pièces (1; 1; 2; 4) car la décomposition du carré d'origine en "petits trangles" ne figure pas sur le triangle rectangle non isocèle ni sur le quadrilatère. On a constaté que les élèves qui travaillent sur un dessin sur quadrillage adoptent volontiers la méthode de "comptage un à un des carreaux" après avoir reconstitué des carreaux entiers avec deux "demi-carreaux" triangulaires ou reconstitué des rectangles 1 x 2 avec deux "demi-rectangles" triangulaires.
3. Inventaire de polygones composés de 2 des 4 pièces de la figure d'origine juxtaposées par des côtés entiers en commun.
Cette dernière activité exige une procédure exhaustive de recherche de toutes les possibilités, et fait appel directement à la reconnaissance de figures isométriques.
Jaquet, F. (2000). Il conflitto area-perimetro / Le conflit aire-périmètre. In L'educazione matematica Anno XXI Serie VI-Vol.2 n.2 (Prima parte pp. 66-77). Anno XXI Serie VI. Vol.3 (Seconda parte pp. 126-143).
Marangoni, E. Sangiorgi, R. (2024). L'importanza del Rally Matematico Transalpino nella Didattica d’aula quotidiana / L’importance des problèmes du Rallye Mathématique Transalpin dans la pratique de classe. In La Gazetta di Transalpino / La Gazette de Transalpie 14. pp 17-24