L'héritage

Identification

Rallye: 08.I.16 ; catégories: 7, 8 ; domaines: GM, GP
Familles:

• CA - Comparer des aires
• CA/D - Comparer des aires par découpage
• DEM - Effectuer une démonstration
• GDE - Organiser une suite de relations en géométrie déductive
• LA - Utiliser des mesures de longueurs et aires

Envoyer une remarque ou une suggestion

Résumé

Observer un rectangle découpé en quatre triangles par quatre segments reliant un point à l’intérieur du rectangle à chacun des quatre sommets. Montrer que la superficie totale des deux triangles dont la base est une longueur du rectangle est équivalente à celle des deux autres triangles (dont la base est une largeur du rectangle).

Enoncé

Tâche de résolution et savoirs mobilisés

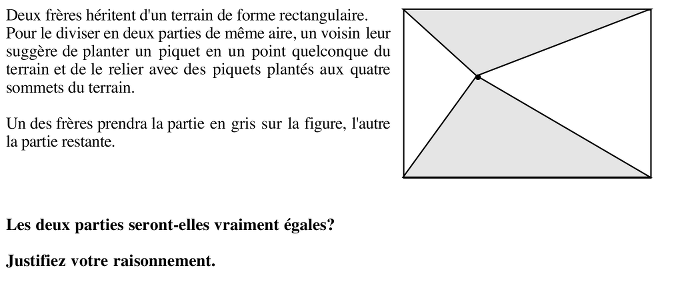
Comprendre que, si on trace les parallèles aux côtés par le point où est planté le piquet, indépendamment de son emplacement, la partie grise et la blanche sont toutes deux composées des quatre mêmes triangles A, B, C, D.

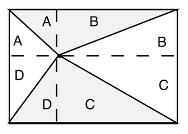
Ou comprendre que pour tout point du rectangle, quatre triangles sont déterminés, ayant deux a deux comme base une des deux dimensions du rectangle et comme somme des hauteurs, l'autre dimension, et que la somme des aires (de deux triangles qui ont bases et hauteurs égales) ne change pas.

Notions mathématiques

aire, rectangle, triangle, longueur, comparaison

Résultats

08.I.16

Sur 60 classes de la section de Suisse romande:

Selon les critères déterminés lors de l’analyse a priori :

• 4 points: Réponse correcte avec procédé démonstratif (du type indiqué dans l'analyse de la tâche)
• 3 points: Réponse correcte à la question avec une erreur logique dans les explications
• 2 points: Réponse correcte avec recours à des exemples (le piquet au centre ou dans d'autres positions)
• 1 point: Réponse correcte avec recours à la mesure ou réponse correcte à la question sans aucune explication
• 0 point: Explications complètement erronées ou incompréhension du problème

Procédures, obstacles et erreurs relevés

Quelques réponses des élèves à la demande de justification

(Les parties sont vraiment égales. Nous avons découpé le rectangle de la figure en différents triangles que nous avons disposés pour obtenir la même figure. Finalement, nous les avons superposés et avons constaté qu'ils étaient vraiment identiques. Ceci est déterminé par le déplacement du centre.)

Trad. Les parties sont vraiment égales. Nous avons découpé le rectangle de la figure en triangles de manière à obtenir la même figure. Puis nous les avons superposées en constatant qu'elles sont vraiment égales. Ceci est déterminé par le déplacement du centre.

La justification est, dans ce cas, du type rapporté dans l’analyse de la tâche.

Si l’on compare les deux exemples, même si les deux réponses sont toutes deux correctes, le niveau des deux raisonnements est conceptuellement différent.

Dans le premier cas, comme on peut le constater, les élèves ont découpé le rectangle en quatre parties, deux blanches et deux grises, et ont recomposé les parties de même couleur pour obtenir deux quadrilatères à comparer. Ils ne justifient cependant pas « formellement » l’équivalence des deux chiffres. Ils se « contentaient » d’un chevauchement, forcément approximatif. Il s'agit en effet d'un argument explicatif local, dans le sens où il "fonctionne" dans ce cas, mais il ne s'étend pas à la considération du fait que quel que soit le choix du point où placer le poteau au sol, l'équivalence entre les deux parties ne change pas. Une situation différente est celle que l’on voit dans le deuxième exemple, où les étudiants justifient formellement l’équivalence. Mais dans une deuxième partie, les élèves passent aux mesures et calculent les aires des deux parties... pour se sentir plus en confiance.

En effet, les élèves de 13/14 ans se trouvent souvent dans une phase de transition entre l'évidence d'une preuve empirique obtenue avec un calcul sur exemple et une justification formelle.

Exploitations didactiques

Après la résolution par groupes et une discussion collective, il faut non seulement que les élèves soient convaincus de l'égalité des deux aires, grise et blanche, mais qu'ils se rendent compte que cette égalité est indépendante de la position du piquet.

Ils doivent constater ou "apprendre" que, ni les estimations, ni les mesures prises à la règle graduée, ni les formules de l'aire des triangles ne leur permettent d'arriver à une certitude en raison de l'impossibilité d'obtenir des mesures précises à la règle graduée.

Ils doivent aussi constater qu'il n'y a pas de décomposition des quatre parties en unités communes puisque les dimensions de ces triangles dépendent de la position du piquet, mais qu'il y a de nombreuses manières de regrouper les triangles:

- Sans les décomposer, il suffit de déplacer le triangle blanc de gauche par une translation de la longueur du rectangle, vers la droite, pour former, avec le triangle blanc de droite un quadrilatère blanc dont les deux diagonales sont perpendiculaires et isométriques respectivement à la longueur et à la largeur du rectangle. Par une translation du triangle noir supérieur de la largeur du rectangle, vers le bas, on obtient également un quadrilatère gris avec les mêmes diagonales que le blanc. Ces deux translations sont élémentaires pour des élèves qui ont l'habitude de manipuler. Il suffit de découper les quatre triangles (et non pas seulement de le dire ou de le faire constater, pour autant que l'enseignant soit convaincu que, jusqu'à l'école secondaire et au lycée, certains élèves ont besoin de travailler sur des objets de leur espace et non seulement sur des figures géométriques!)

- En décomposant les quatre triangle en huit triangles rectangles (comme le propose la rubrique "Tâche de résolution et savoirs mobilisés) on arrive aussi à se convaincre de l'égalité des parties blanche et grise.

Sans manipulations ni déplacements de figures, l'exploitation didactique serait absolument insuffisante pour des élèves qui n'ont pas trouvé l'égalité des deux parties du terrain ni n'ont su l'expliquer. Et, pour profiter de ce travail manuel, les élèves pourront se convaincre que les égalités sont vérifiées quelque soit l'emplacement du piquet.

L'enseignant peut profiter de l'activité pour revoir le concept de translation et d'isométrie, qui s'applique tant aux longueurs des côtés et aux aires. Il peut aussi faire constater aux élèves qu'il y a un moyen très simple de trouver l'aire d'un quadrilatère dont les deux diagonales sont perpendiculaires: c'est la moitié de l'aire du rectangle circonscrit.

Bibliographie

Grugnetti L. 2001. «Dimostrazione» e prove empiriche in problemi di geometria del RMT / «Démonstration» et preuves empiriques dans les problèmes de géométrie du RMT. In Atti del RMT / Actes du RMT. Vol. 2. pp 25 - 37