
Banque de problèmes du RMT
ud262-fr
 |
Banque de problèmes du RMTud262-fr |
|
Déterminer les dimensions de deux rectangles en carton pesant respectivement 48 et 30 grammes sachant que la longueur du second vaut les 3/4 de la longueur du premier et que la largeur du second mesure 10 cm.

- Comprendre que l'aire des rectangles est proportionnelle à leur masse et que le rapport des aires du premier et du second est 48/30
- Le rapport des longueurs étant 4/3, le rapport k des largeurs sera tel que 4/3 x k = 48/30 et en déduire que k = 48 /30: 4/3 = 48 / 30 x 3/4 = 6 /5
- La largeur du premier mesure donc 6/5 x 10 = 12
- Par une méthode arithmético-géométrique, le problème se résout ainsi : si l'aire du grand était de 48 unités d'aire, correspondant chacune à un rectangle-unité (de 1 gramme, de largeur 1 cm et de longueur u cm) l'aire du petit en vaudrait 30.
Les 30 unités d'aire du petit se répartissent dans le petit rectangle de 10 cm de largueur, de longueur 3u ( inconnue).
La longueur du grand rectangle, qui est les 4/3 de celle du petit aura donc une longueur de 4u. Pour une aire totale de 48, cela représente x = 12 cm de largeur
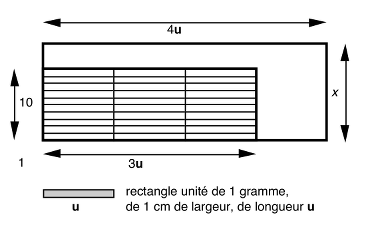
- Il y a encore d'autres méthodes possibles, faisant appel à des représentations géométriques, mais on ne connaîtra jamais les longueurs des rectangles, car elles dépendent de la masse du papier par unité d'aire, ce qui n'est pas dit dans l'énoncé.
rectangle, longueur, largeur, équation
Les résultats n'ont pas été conservés ou ne sont pas encore disponibles.
(c) ARMT, 2000-2024