Tours de 18 cubes

Identification

Rallye: 20.F.10 ; catégories: 5, 6, 7 ; domaine: 3D
Familles:

• VS - Visualiser dans l'espace
• VS/OA - Compter ou dénombrer des objets

Remarque et suggestion

Résumé

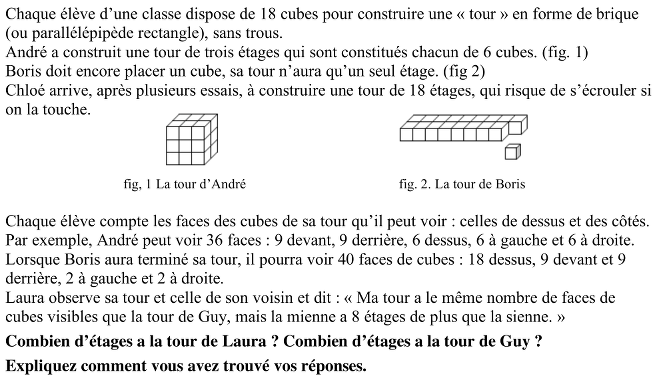
Déterminer les parallélépipèdes rectangles formés de 18 cubes posés sur une table dont le nombre de faces visibles est le même mais dont la différence "d'épaisseur" est 8.

Enoncé

Tâche de résolution et savoirs mobilisés

Analyse a priori

- Comprendre que, pour trouver les tours des deux élèves, une possibilité est d’envisager toutes les constructions possibles de 36 cubes, en forme de p.r. en fonction de la « base » (face inférieure non visible) et espérer qu’on en trouvera deux qui aient le même nombre de faces visibles.

Voici cet inventaire, organisé de la tour de 18 étages à celles de 1 étage :

On trouve 10 tours, de 6 hauteurs et 10 rectangles de base. Il n’y a que 8 nombres de faces visibles différents : 33 36 36 40 48 49 51 56 56 73

Il y a deux tours avec 36 faces visibles, de 1 et 3 étages et deux autres avec 56 faces visibles, de 1 et 9 étages.

C’est donc ces deux dernières tours qu’il faut prendre en considération car elles ont 8 étages de différence. C’est la tour de Laura qui a 9 étages et celle de Guy qui n’en a que 1.

Ou, en considérant la décomposition de 18 en facteurs (1, 2, 3, 6, 9, 18), dont l’un sera le nombre d’étages, constater qu’une différence de 8 étages ne peut exister qu’entre deux tours : celle de 1 et 9 étages… et vérifier.

Notions mathématiques

opération, décomposition d’un nombre, nombre naturel, produit, facteur, rectangle, aire, périmètre, volume

Résultats

20.F.10

Points attribués sur 153 copies de 17 sections:

Selon les critères déterminés lors de l’analyse a priori :

• 4 points: Réponse exacte et complète (Laura 9 et Guy 1) avec explications claires qui permettent de justifier l’unicité de la solution (inventaire complet, raisonnement sur les diviseurs de 18, …)
• 3 points: Réponse exacte et complète avec des explications qui ne permettent pas de justifier l’unicité de la solution, mais avec une vérification
  ou inventaire incomplet (manquent de 1 à 3 tours) mais permettant toutefois d’obtenir les deux tours recherchées dont 56 faces sont visibles
• 2 points: Réponse exacte et complète sans aucune explication
  ou inventaire incomplet (manquent de 1 à 3 tours) ne permettant pas de voir les deux tours recherchées
  ou une ou deux erreurs de calculs dans l’inventaire complet, cohérent avec la réponse
  ou inventaire complet mais en comptant les faces invisibles de la base
• 1 point: Recherche de quelques tours seulement avec un calcul correct des faces visibles
• 0 point: Incompréhension du problème

(c) ARMT, 2012-2024