Quanti parallelogrammi

Identificazione

Rally: 22.F.09 ; categorie: 5, 6, 7 ; ambito: GP
Famiglie:

• IF - Identificare figure
• IF/INV - Fare un inventario

Envoyer une remarque ou une suggestion

Sunto

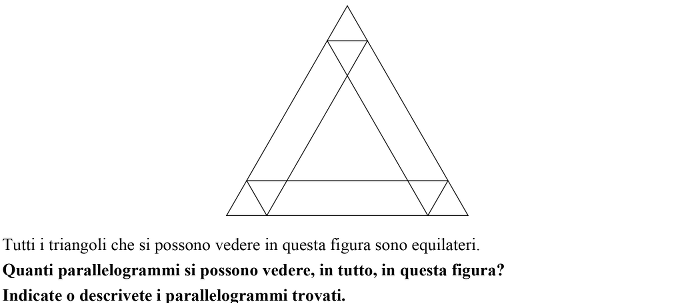
Riconoscimento e conteggio di parallelogrammi in una figura.

Enunciato

Compito per la risoluzione e saperi mobilizzati

Analyse a priori

- Saper riconoscere dei parallelogrammi in una figura, tenendo conto del carattere regolare della figura per identificare i parallelogrammi uguali;

- organizzarsi per non dimenticare nessun parallelogramma e per non contare due volte lo stesso.

- Sfruttare il fatto che in un parallelogramma i lati opposti sono paralleli.

- Scegliere due paia di lati paralleli al fine di formare un quadrilatero che sarà obbligatoriamente un parallelogramma.

- Considerare che il rombo è un parallelogramma.

Ci sono evidentemente molti modi di organizzare l’inventario, con numerosi rischi di confusioni o di dimenticanze:

- assegnare una lettera a tutti i vertici della figura (o ai segmenti) e designare i parallelogrammi con questi vertici (o questi segmenti), ciò che porta ad una notazione pesante e lunga, difficile da controllare,

- utilizzare dei colori per ripassare i contorni, cosa che non permette di distinguere i vari segmenti,

- lavorare per tipi di parallelogrammi in un modo diverso da quelli finora descritti, tenendo conto per esempio delle trasformazioni del triangolo equilatero …

Il compito principale è appunto quello di scegliere la rappresentazione più efficace.

Si arriva a:

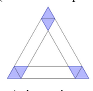
- 3 parallelogrammi che sono anche dei rombi (1 famiglia di parallelogrammi)

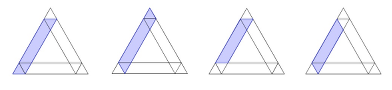
- 12 parallelogrammi (che non sono dei rombi), cioè

3 famiglie di 4 parallelogrammi, una volta a sinistra come nella figura

una a destra e una in basso.

Ci sono in tutto 3 + 12 = 15 parallelogrammi.

Risultati

22.F.09

Punteggi attribuiti su 194 classi di 22 sezioni:

Secondo i criteri dell’analisi a priori:

• 4 punti: Risposta completa (15) con descrizione completa (disegno o altre descrizioni)
• 3 punti: Risposta corretta (15) con descrizione poco “leggibile” (per esempio, con colori sopra uno stesso disegno o altre descrizioni che non illustrano tutti i parallelogrammi)
• 2 punti: Risposta (15) senza alcuna descrizione o (13) o (14) con descrizione (una o due dimenticanze)
  oppure risposta sbagliata (12) per la dimenticanza dei tre parallelogrammi rombi, con descrizione
  oppure risposta più di 15 per la presenza di altre figure non corrette (es. trapezio non parallelogramma)
• 1 punto: Da 4 a 11 parallelogrammi differenti
• 0 punto: Meno di 4 parallelogrammi o incomprensione del problema