La piramide di Sofia

Identificazione

Rally: 23.F.17 ; categorie: 9, 10 ; ambito: 3D
Famiglie:

• LAV - Gestire lunghezze, superfici, volumi
• RD - Ricercare o utilizzare dimensioni
• RD/PY - Utilizzare una relazione classica

Remarque et suggestion

Sunto

In una piramide regolare con gli spigoli tutti congruenti determinare gli spigoli di un parallelepipedo rettangolo a base quadrata posizionato all’interno della piramide.

Enunciato

Compito per la risoluzione e saperi mobilizzati

Analisi a priori

- Capire che le facce laterali della piramide sono triangoli equilateri.

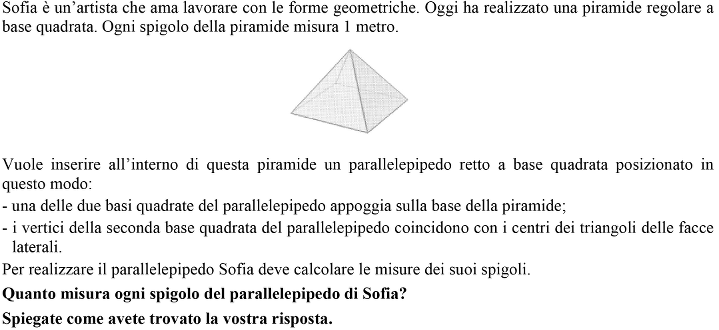
- Capire che la posizione dei vertici del parallelepipedo può essere ottenuta tagliando la piramide con un piano che passa per l’altezza CO della piramide e per il punto medio H di uno spigolo di base.

Sono possibili due strategie:

1. Strategia basata su proprietà e teoremi e sul calcolo:

Indicato con M il centro di ogni faccia laterale e con N il piede della perpendicolare condotta da M alla base della piramide, si ottiene uno spigolo laterale, MN, del parallelepipedo.

Comprendere che ON è uguale alla metà della diagonale della base quadrata del parallelepipedo.

Detta CAB una faccia laterale della piramide, ricordare che il centro M dista da H un terzo di CH, e dunque si ha:

$MH = \frac{CH}{3} = \frac{1}{3}\frac{\sqrt{3}}{2}BC = \frac{\sqrt{3}}{6} $(in metri)

Si può determinare la misura MN applicando il teorema di Talete o per la similitudine dei triangoli OCH e NMH:

$OH = AB/2 = 0,5$ (in metri), quindi per il teorema di Pitagora:

$OC = \sqrt{CH^2 - OH^2} = \sqrt{\frac{3}{4} - \frac{1}{4}} = \frac{\sqrt{2}}{2}$ metri

Dunque:

$MN/OC = MH/CH \Rightarrow MN=OC \times MH/CH = \frac{\sqrt{2}}{6}$ (in metri)

$NH/OH = MH/CH \Rightarrow NH=OH \times MH/CH = \frac{1}{2} \times \frac{1}{3} = \frac{1}{6}$

$ON = OH – NH = 1/2 – 1/6 = 2/6$ (in metri) e $2 ON = 4/6 = 2/3$ (in metri)

La diagonale del quadrato di base del parallelepipedo misura 2/3 (in metri) e la sua base misura $\frac{\sqrt{3}}{2}$

Dunque gli spigoli del parallelepipedo misurano rispettivamente metri (approssimando al centimetro: 0,47 metri) e metri (cioè approssimando al centimetro: 0,24 metri).

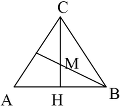
Altra possibilità per determinare la misura dello spigolo di base del parallelepipedo:

ABFE è la base della piramide e NPRL la base del parallelepipedo rettangolo.

Per il teorema di Talete: $ON/OH = NP/HI$ dunque

$NP = ON/OH \times HI =\frac{2}{3} \times \frac{\sqrt{2}}{2} = \frac{\sqrt{3}}{2}$

2. Strategie basate su proprietà, disegno e misura:

- Rappresentare il triangolo ACB per esempio in scala 1/10, disegnare due delle tre mediane dopo aver individuato il centro del triangolo e misurare MH approssimando al mm.

- Calcolare OC, e disegnare il triangolo rettangolo OCH. Riportare con il righello o con il compasso la lunghezza di MH su CH, disegnare e misurare MN.

- Disegnare il quadrato OHAI o il quadrato AEFB e le sue mediane, utilizzare il righello o il compasso per individuare N su OH e P su OI e misurare NP.

Risultati

23.F.17

Su 43 classi di 8 sezioni partecipanti alla prova finale del 23° RMT:

Secondo i criteri dell’analisi a priori:

• 4 punti: Risposta corretta ($\frac{\sqrt{2}}{3}$ e $\frac{\sqrt{2}}{6}$ oppure 0,47 e 0,23 o 0,24 in metri o 47,1 cm e 23,6 cm) con spiegazioni chiare
• 3 punti: Risposta corretta con spiegazione incompleta o con valori approssimati diversi ottenuti da approssimazioni effettuate fin dai primi calcoli)
  oppure risposta non corretta dovuta solamente ad un errore di calcolo, ma con opportune spiegazioni.
• 2 punti: Risposta incompleta, ma con chiari segni di comprensione del problema (per esempio, tener conto del centro di gravità del triangolo e della sezione della piramide).
• 1 punto: Inizio di ragionamento corretto che fa intendere la comprensione del problema (per esempio, calcolo esatto della misura dell’altezza della piramide).
• 0 punto: Incomprensione del problema.

(c) ARMT, 2015-2024