calculs de compression

Systèmes de communication

Quelques calculs de compression (2)

Codage de Huffman

Recherche d'un code de Huffman pour le fichier contenant: E(35), N(10), T(8), S(11), X(2), R(7), O(27)

Lettre	%	Code	longueur	longueur pondérée
E	.35	0	1	.35
O	.27	10	2	.54
S	.11	110	3	.33
N	.10	1110	4	.40
T	.08	11110	5	.40
R	.07	111110	6	.42
X	.02	111111	6	.12

Nombre moyen de bits par lettre: 2.56 (contre 3 pour un codage de longueur fixe). Mais il est possible de faire plus économique en utilisant l'algorithme représenté par la figure:

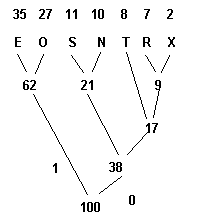
Lettre	%	Code	longueur	longueur pondérée
E	.35	11	2	.70
O	.27	10	2	.54
S	.11	011	3	.33
N	.10	010	3	.30
T	.08	001	3	.24
R	.07	0001	4	.28
X	.02	0000	4	.08

Nombre moyen de bits par lettre: 2.47 (contre 2.56 précédemment)

Note: La théorie indique que pour un fichier contenant des caractères stochastiquement indépendants avec les probabilité p_i d'apparition le nombre de bits par symbole tend vers l'entropie:

Technique LRE

Dans un mode graphique (ancienne technologie) avec 1 bitplane à 4 bits par pixel (16 couleurs), on a une résolution de 640x480 points. On représente sur l'écran un damier de 16 sur 16 cases. Deux cases adjacentes sont supposées avoir des couleurs différentes.

a) Grosseur d'un fichier "RAW" de la mémoire graphique (on suppose mettre 2 pixels par byte):

Nombre de pixels: 640 * 480 = 307200
Nombre de bytes: 307200 / 2 = 153600
Grandeur du fichier: environ 154 kB.

b) Taille approximative d'un fichier de type PCX (sans compter l'en-tête, en général de 128 bytes).

Nombre de bytes pour 16 pixels (de la même couleur): 2
Nombre de paquets de 16 pixels: 640 * 480 / 16 = 19200
Nombre de bytes total: 19200 * 2 = 38400
Grandeur du fichier: environ 39 kB

Compression topographique

V est la taille d'un fichier en octets et N est le nombre de 0 contenus dans ce fichier.

Taille du fichier compressé par compression topographique (sans compter l'entête):

Nombres de bytes pour la partie "topographique": V/8
Nombres d'octets restants: V - N
Dimension du fichier compressé en bytes: V - N + V/8

Compression maximale possible:

Elle a lieu lorsque tous les éléments dont des 0. Taille du fichier compressé: V/8

Compression minimale possible:

Aucun élément n'est 0; le fichier "gonfle": V+V/8