coeff locaux

Ces concepts à leur tour peuvent être des descripteurs d'autres unités d'information. L'introduction de types de concepts permettra par la suite de proposer une structuration de l'ensemble des unités d'informations accumulées.

Notations et coefficents numériques

En suivant et généralisant [BAL 90], on introduit le formalisme suivant:

U = {u₁, u₂, ..., u_t} ;le nombre d'élément de U est désigné par t = #U = Card(U) ;
C = {c₁, c₂, ..., c_s} ;le nombre d'élément de C est désigné par s = #C = Card(C) ;
N = Card(D) ;
N* = Card(D*) ;

Par ailleurs, on s'intéressera aux différentes "projections" (en se référant à une représentation graphique telle que celle de la figure 1) des relations d et d*.

U(c) = {u | d(c,u) } U est l'ensemble des unités d'information dont c est descripteur;
D(u) = {c | d(c,u) } C est l'ensemble des descripteurs de l'unité d'information u ;
U*(c) = {u | d*(c,u) } U est l'ensemble des unités d'information faisant appel au concept c. (comptée une seule fois !) ;
D*(u) = {c | d*(c,u) } C est l'ensemble des concepts référents dans u.

On rappelle que ces définitions sont ensemblistes, elle ne tiennent pas compte de la réalisation topologique. Une unité d'information peut être la "cible" (physique) de plusieurs liens liés au même concept, mais elle n'apparaît qu'une fois dans l'ensemble U(c) ! (5)

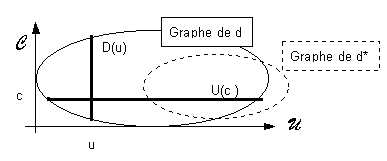
Figure 1: Représentation des relations d et d* dans un plan cartésien. Les différents ensembles définis correspondent à des coupes des graphes de d et de d*.

On pourra aussi se représenter un hypertexte en juxtaposant deux "produits" cartésiens C x U.

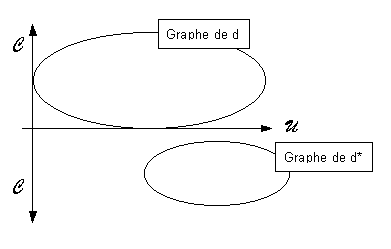
Figure 2: Représentation des relations d et d* dans deux "plans" juxtaposés.

Les cardinaux de ces ensembles ont tous une signification particulière:

Re(c) = Card(U(c)) : rendement ou valence du concept c, nombre d'unités d'information décrite par c ;
Re*(c) = Card(U*(c)) : répartition du concept c, nombre d'unités d'information ayant c comme référent ;
Di(u) = Card(D(u)) : disponibilité de u, nombre de concepts "descripteur" de u ;
Di*(u) = Card(D*(u)) : ouverture de u, nombre de concepts "référent" dans u.

On a les égalités (I):

_c Re(c) = _u Di(u ) = Card({(c,u) | d(c,u) }) = N

_c Re*(c) = _u Di*(u ) = Card({(c,u) | d*(c,u) }) = N*

On définit encore les notions relatives:

Rr(c) = Re(c) / N : rendement relatif du concept c (_c Rr(c) = 1) ;
Rr*(c) = Re*(c) / N* : répartition relative de c ;
Dr(u) = Di(u) / N : disponibilité relative de l'unité u ;
Dr*(u) = Di*(u) / N* : ouverture relative du référent de u.

De plus on note les valeurs moyennes pour un hypertexte:

Rm = _c Re(c)/#C= N/#C : rendement moyen ;
Rm* = N*/#C : la répartition moyenne ;
Dm = _u Di(u)/#U = N/#U : la disponibilité moyenne ;
Dm* = N*/#U : l'ouverture moyenne.

Pour une unité et un concept on définit les rapport:

E(u) = Di*(u) / Di(u) : balance de u (sortant sur rentrant) (6) ;
C(c) = Re*(c) / Re(c) : balance de c ;

Si on définit la notion relative: Er(u) = Dr*(u)/Dr(u), on a: Er(u) = E(u) (N/N*).

Notation matricielle

Les relations peuvent aussi être représentées par des matrices (à valeur 0 ou 1). La matrice correspondant à d sera notée D et celle correspondant à d* sera notée R. Chaque ligne des ces matrices représentera un document et chaque colonne un concept.

On laisse au lecteur le soin de constater que les différents coefficients locaux défininis peuvent s'exprimer en terme de sommes de lignes et de colonnes des matrices R et D.

Cas particuliers

Quelques valeurs extrêmes permettent d'avoir une meilleure appréhension des coefficients introduits. Le tableau 1 donne quelques interprétations de valeurs particulières de ces coefficients.

Tableau 1: Interprétation de quelques valeurs particulières des coefficients: Re, Re*, Di et Di*

Re(c) = 0
C(c) =
Le concept est une "question sans réponse", il n'est pas descripteur (concept minimal, considéré mais non défini).

Re(c) = 1 L'unité u telle que U(c) = {u} est une illustration ou une définition du concept de c. Si de plus D(u) = {c}, il s'agit d'une note, par exemple.

Re(c) = #U C'est la valeur maximale que peut atteindre Re(c). Dans ce cas le concept n'a aucune valeur discriminante.

Di(u) = 0
E(u) =
Le noeud est une unité isolée, une "source" ce qui est le cas d'une unité racine (table des matières, par exemple).

Di(u) = 1 Indique que u n'a qu'un seul descripteur, ce qui est une situation assez courante.

Di(u) = #C C'est la valeur maximale que peut atteindre Di(u). Tous les concepts sont descripteur de u.

Re*(c) = 0
C(c) = 0
Le concept n'apparaît pas comme référent.

Di*(u) = 0
E(u) = 0
L'unité d'information est sans référent, un "puit" qui correspond à une unité terminale (feuille).

C(c) = 1 Re(c) = Re*(c). Le concept c est descripteur autant de fois qu'il est référent.

E(u) = 1 Di(u) = Di*(u). Il y a autant de descripteurs que de référents pour u.

Exemples

Les valeurs des coefficients seront calculées pour deux exemples typiques, l'un en "largeur" et l'autre en "profondeur": une base de donnée "classique" et une arborescence.

1) Base de données "classique"

Elle sera donnée par n fiches contenant p champs. Chacun représente un concept c (par exemple: nom, prénom, adresse, etc.).

2) Arborescence (fig 3)

Chaque unité d'information, sauf celles qui sont terminales contient un menu avec rubriques, chacune représentant un concept unique. Chaque rubrique, conduit à une unité d'information. L'arbre a une profondeur de +1 ( 1).

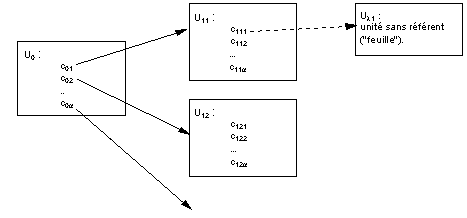
Figure 3: Organisation de l'information sous forme d'arbre (système de menus)

Nombre de concepts p' = + ² + ... + = ( -1)/( - 1)

Nombre d'unités d'information: n' = 1 + p'

Le tableau 2 présente les valeurs des coefficients pour ces deux cas particuliers.

Tableau 2: Coefficients pour deux hypertextes simples

#U #C N N*

Base de données n p np 0

Arborescence 1+p' p' p' p'

Re(c) Re*(c) Di(u) Di*(u)

Base de données n 0 p 0

Arborescence 1 1 0 pour racine; 1 sinon ; 0 pour terminale

Rr(c) Rr*(c) Dr(u) Dr*(u)

Base de données 1/p indéfini 1/n indéfini

Arborescence 1/p' 1/p' 0 pour racine ; 1/p' /p' ; 0 pour terminale

Rm Rm* Dm Dm*

Base de données n 0 p 0

Arborescence 1 1 p'/n' 1 p'/n'

E(u) C(c)

Base de données 0 0

Arborescence pour racine ; ; 0 pour terminale 1

Ce schéma permet de comparer, par exemple, un système de fiches d'adresses organisé tout dabord comme un ensemble de fiches séparées avec nom et adresse (p = 2) et sous la forme d'une liste de noms avec un lien sur l'adresse ( = n, = 1, donc p' = = n, n' = 1 + n). Les coefficients dépendent de la structure choisie et non de l'ensemble des unités d'information en présence.

En définitive, le modèle utilisé permet de rendre compte d'un certain nombre de structures et donne un cadre à l'utilisation d'une famille de coefficients classiques tels que ceux définis par [BAL 90]. Ce modèle offre un "instantané"; s'il s'agissait de prendre en compte certains outils de navigations et plus généralement des liens calculés, il faudrait considérer ces valeurs comme fonction du temps et de donner des règles de transition.

Notions dérivées

Distance et corrélation

Dans les problèmes d'indexation des documents chaque document est caractérisé par un vecteur. On notera ici: v(u) = (<u,c>)_cC . Le poids <u,c> peut être donné par diverses formules dont celle de Salton (citée par [BAL 96 p 107] et [SME 96 p 6])

<u,c> = occ(c,u) log (#C / Re(c))

où occ(c,u) est le nombre de fois où le concept c apparaît dans l'unité d'information u.

Mais ce coefficient peut aussi être "subjectif" (intérêt) ou encore tenir compte de l'information référencée. Par ailleurs, dans notre perspective, l'indexage du document contient en plus le contenu référent qui donne lieu à un autre poids <u,c>*. De façon duale, on peut aussi considérer les profils des concepts (<u,c>)_uU.

Dès ce moment, il est possible de définir sur l'ensemble des unités d'information produit scalaire, corrélation, distance "euclidienne", voire d'autres distances. Dans notre cas, sauf indication contraire, <u,c> est donné par 1 si c est un descripteur de u et 0 sinon. De même pour <u,c>*.

Quant à la distance, on utilisera principalement le nombre de désaccords et le pourcentage de désaccords (cette deuxième mesure de l'écart est également une distance (7) ). C'est-à-dire que la distance entre u1 et u2 sera:

(u1,u2) = Card ( D(u1) D(u2) ) (8)

ou dans le cas "relatif":

_r(u1,u2) = Card ( D(u1) D(u2) ) / Card (D(u1) D(u2)) (9)

Le poids d'une unité d'information (sa longueur ou sa distance à l'unité d'information vide) est donné par |u| = (u,0) = _cC <u,c> = Di(u).

La corrélation de deux unités d'information est donnée par le produit scalaire des vecteurs correspondant. Dans notre cas par:

(u1,u2) = Card ( D(u1) D(u2) ) / Card (D(u1) D(u2)).

On a: (u1,u2) = 1 - _r(u1,u2).

Ces définitions peuvent également s'utiliser avec les référents:

*(u1,u2) = Card ( D*(u1) D*(u2) ) / Card (D*(u1) D*(u2)).

On a encore dans le cas " pourcent de désaccords ": *(u1,u2) = 1 - _r*(u1,u2).

et * correspondent aux notions de couplage classiques introduites par Kessler et Weinberg (selon [SAV 96]).

Les mêmes notions sont également utilisables entre les concepts:

_r(c1,c2) = Card ( U(c1) U(c2) ) / Card (U(c1) U(c2))

(c1,c2) = 1 - _r(c1,c2) = Card ( U(c1) U(c2) ) / Card (U(c1) U(c2))

Même chose pour *_r et * .

Relations dérivées et lien avec la théorie des graphes

Tout d'abord mentionnons que l'on peut considérer les graphes bipartites correspondant aux relations d et d*. Dans ce cas, Re(c) correspond à l'ordre du sommet c et Di(u) à l'ordre du sommet u.

Relation ternaire sur U x C x U : du(u,c,u') si et seulement si d*(c,u) et d(c,u'). Cette relation est celle considérée dans [LUC 96]. On le verra ultérieurement, cette relation permet d'induire un type sur les liens entre unités d'information.

De même on définira une relation sur C x U x C : dc(c,u,c') si et seulement si d(c,u) et d*(c',u).

Quant au graphe classique [FUR 96] entre les unités d'information, il dépend de la relation dérivée suivante:

Relation induite sur U : ru(u,u') ssi il existe c tel que d*(c,u) et d(c,u'). Le graphe orienté associé à cette relation est utilisé par [FUR 96] pour comparer les hypertextes. On le notera: Gu(H). En général on impose que le graphe associé soit faiblement connexe. Cette relation peut s'exprimer sous la forme d'un calcul matriciel : la matrice G_U (associée à ru) ayant en ligne i et colonne j le nombre de liens de u_i vers u_j est le produit de R (matrice documents x référents) et D' (transposée de D matrice documents x descripteurs). G_U= RD'.

On notera S(u,u') = 1 si ru(u,u') et S(u,u') = 0 sinon.

Par ailleurs, M(u,u') = Card { c C | du(u,c,u') }. Les nombres M(u,u') sont les coefficients de G_U.

M(u,u') indique le degré de connexion de deux unités u et u'. S(u,u') indique simplement s'il y a connexion ou pas.

De même on considérera la relation induite sur C : rc(c,c') ssi il existe u telle que d(c,u) et d*(c',u). On dira dans ce cas que c' est un sous-concept de c, ou que c dépend de c'. (c est descripteur de u et c' fait partie du référent de u). Le graphe associé est Gc(H). Cette relation peut s'exprimer sous la forme d'un calcul matriciel : la matrice G_C = R'D ayant en ligne i et colonne j le nombre de connexions entre c_i et c_j , est le produit de R' (transposée de la matrice document x référents) et D (matrice documents x descripteurs).

Les mêmes coefficients peuvent être introduits pour les concepts: S(c,c') = 1 si rc(c,c') et S(c,c') = 0 sinon.

Par ailleurs, M(c,c') = { u U | dc(c,u,c') }.

M(c,c') indique le degré de connexion de deux concepts c et c'. S(c,c') indique simplement s'il y a "connexion" entre les concepts ou pas. Ces coefficients joueront un rôle lors du double typage (descripteur et référent) par regroupement des concepts.

Les autres coefficients qui peuvent être introduits:

Valence ou rendement d'une unité d'information (liens sortants de u)

VS*(u) = Card {u' U | ru(u,u') } = _u' S(u,u') = nombre d'arêtes du graphe d'origine u.

VM*(u) = _{c

D*(u)} Re(c) = _u' M(u,u'). (prise en compte de la multiplicité).

On a : VS*(u) VM*(u) Di*(u) VS*(u)

Disponibilité totale d'une unité d'information (liens rentrants)

VS(u) = Card {u' U | ru(u',u) } = _u' S(u',u) = nombre d'arêtes du graphe "pointant" sur u.

VM(u) = _{c

D(u)} Re*(c) = _u' M(u',u)

VS(u) VM(u) Di(u) VS(u)

Notion de corrélation moyenne

Ce qui précède suggère de définir:

comme une corrélation moyenne des référents liés à l'unité d'information u. Ce coefficient est compris entre 1/Di*(u) et 1. Plus r*(u) est grand, et plus les liens sortants conduisent aux mêmes unités d'information.

Dans le cas où D*(u) = {c1, c2}, on a:

r*(u) = (c1,c2) / (1 + (c1,c2)) avec, on le rappelle:

(c1,c2) = Card(U(c1) U(c2)) / (Card (U(c1) Card(U(c2) )

r* est donc bien lié à une corrélation de concepts. Il est sensible à la valeur de Di*(u) (comme tous les coefficents de corrélation) surtout pur les petites valeurs (un correctif valant Di*(u)/(Di*(u)-1) pourrait être introduit).

De même, le coefficient dual peut être introduit:

Il représente une corrélation moyenne des descripteurs de u. Les valeurs de r sont comprises entre 1/Di(u) et 1. Plus r(u) est grand, et plus les liens entrants proviennent des mêmes unités d'information.

Ramification de c

RS*(c) = Card {c' C | rc(c',c) } = nombre d'arêtes du graphe d'origine c. Ce nombre est Inférieur ou égal à _{u

U*(c)} Di(u) = RM*(c). Par ailleurs:

RM*(c) Re*(c) RS*(c)

Propagation de c

RS(c) = Card {c' C | rc(c,c') } = nombre d'arêtes du graphe "pointant" sur c. Ce coefficient est inférieur ou égal à RM(c) = _{u

U(c)} Di*(u). Par ailleurs,

RM(c) Re(c) RS(c)

Notion de corrélation moyenne

r(c) = (Re(c)/(Re(c) - 1) ) (1 - RS(c)/RM(c)) corrélation moyenne des unités d'information décrites par c.

r*(c) = (Re*(c)/(Re*(c) - 1) ) (1 - RS*(c)/RM*(c)) corrélation moyenne des unités d'information contenant le référent c.

VX(u) = VX*(u) = RX(c) = RX*(c) = nombre d'arêtes des deux graphes associés.

On définit également VX*(u)/VX(u) et RX*(c)/RX(c).

VX*(u)/VX(u) constitue une approximation de premier ordre de la "balance", c'est-à-dire du rapport entre les unités d'informations attachées à u et celles auxquelles u est attachée (6).

Le tableau 3 donne les valeurs des coefficients dérivés pour les deux cas particuliers de la "base de données" et de l'arborescence. Les valeurs 0 sont typiques d'unités isolées et de concepts sans sous-concept.

Tableau 3: Coefficients dérivés pour la base de données simples et l'arborescence

VS(u) VS*(u) RS(c) RS*(c)

Base de données 0 0 0 0

Arborescence 0 pour ui racine ; 1 sinon ; 0 pour ui terminale 0 pour concept racine; 1 sinon ; 0 pour concept terminal

Notes

1) d correspond à l'association classique " mot-document ".

2) Il n'y a évidemment a priori aucun rapport entre les relations d et d* et les relations permettant de configurer une base de données relationnelle.

3) On notera parfois: c1 < c2 ; si U(c1) U(c2) (c2 décrit au moins toutes les unités d'information décrites par c1) et u1 u2 ; si D(u1) D(u2) (les descripteurs de u1 sont tous des descripteurs de u2)

4) Un concept est à prendre au sens large, il pourrait tout aussi bien s'agit d'un mot, d'une expresssion plus complexe, d'un type d'argumentation, etc.

5) De ce point de vue formel, un hypertexte est constitué de deux parties qui se correspondent l'une à l'autre comme espace vectoriel et espace affine associé. La partie "vectorielle" considère l'existence de relations entre concepts et unités d'information du point de vue ensembliste. La partie "affine" tient compte de la réalisation physique d'un hypertexte. Elle considère la répartition d'un même concept dans les unités d'information et, de façon duale, le nombre de fois où une unité d'information est décrite par un concept donné.

6) On retrouve ici l'idée de bilan informationnel introduit par Yona Friedman [ESC 76] à propos de la transmission de l'information dans un groupe. Dans ce cas on considérerait plutôt le bilan additif: Di*(u) -Di(u)

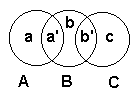
Dans le cas le plus défavorable:

_r(A,C) = 1 ;
_r(A,B) = (a+b+b')/(a+a'+b+b') = 1 - a'/(a+a'+b+b');
_r(B,C) = (a'+b+c)/(a'+b+b'+c) = 1 - b'/(a'+b+b'+c)
et _r(A,C) est inférieur à _r(A,B) + _r(B,C)

8) D'autres distances peuvent être utilisées, par exemple la distance euclidienne: (u1,u2) = (_c (<u1,c> - <u2,c>)² )^1/2. Dans le cas où <u,c> vaut 1 ou 0 selon que c est dans u ou non, les distances sont équivalentes. En l'occurence dans le cas euclidien: (u1,u2) = Card (D(u1) D(u2)) ^1/2. Son poids est Di(u)^1/2.

9) Pour la commodité des calculs on utilise parfois Card (D(u1)) + Card(D(u2)).