
Banca di problemi del RMT
3d10-it
 |
Banca di problemi del RMT3d10-it |
|
Costruire scatoline ritagliando e incollando i rettangoli dati. Dichiarare quanti e quali rettangoli servono e quali sono stati i criteri usati per affrontare la ricerca ai fini di un’ assemblaggio corretto.
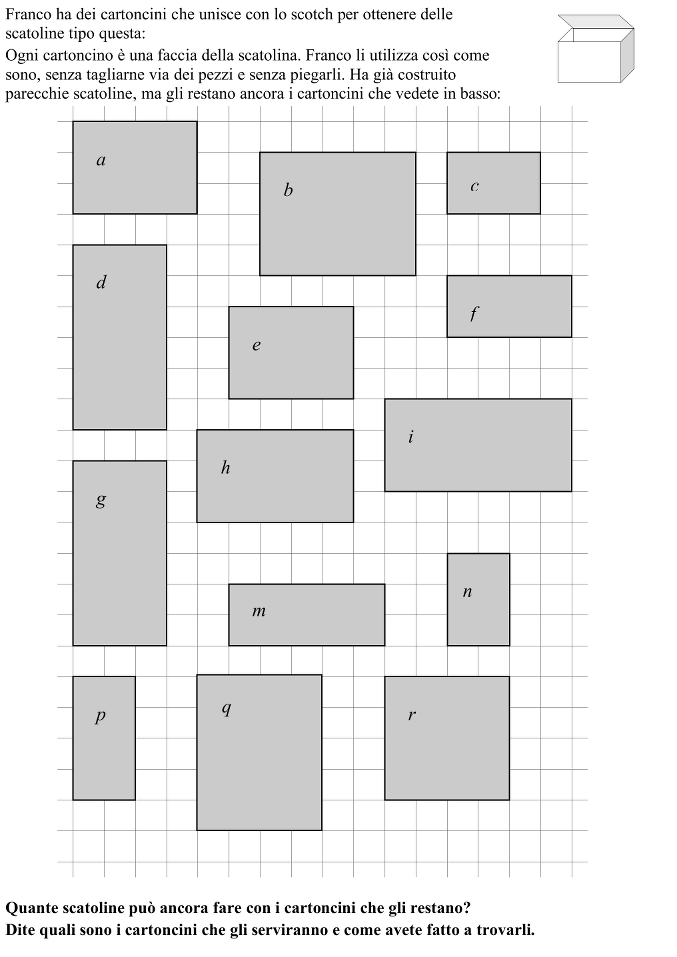
Ritagliare i rettangoli e ricostruire la scatolina come in un puzzle.
Comprendere che ogni scatola è composta da 6 facce e che, in una scatola di questa forma ( parallelepipedo rettangolo), le facce opposte sono dei rettangoli uguali (isometrici o sovrapponibili).
Raggruppare, per esempio, i cartoncini con le stesse dimensioni : a e e; b e q; c e n; d, g e i; f e p; e osservare che h, m e r restano soli, con questa classificazione e sono quindi da eliminare.
Capire che bisogna inoltre escludere, tra i cinque gruppi formati precedentemente, i cartoncini d, g, i, un lato dei quali vale 6, perché nessun’altra coppia ha dei lati di questa lunghezza e i cartoncini b, q, un lato dei quali vale 5, perché nessun’altra coppia ha dei lati di questa lunghezza.
Capire quindi che la sola scatolina costruibile sarà composta dai cartoncini a, e p, f c, n .
Dedurne che i cartoncini rimasti non danno la possibilità di costruire una seconda scatola.
Costruire con i cartoncini scelti una scatola o disegnarla.
costruzione di un modello, passaggio dalle piano alle spacio, congruenza fra rettangoli
| Categoria | 0 | 1 | 2 | 3 | 4 | Nb.classi | Media |
|---|---|---|---|---|---|---|---|
| Cat 3 | 113 (60%) | 27 (14%) | 11 (6%) | 27 (14%) | 10 (5%) | 188 | 0.9 |
| Cat 4 | 107 (54%) | 26 (13%) | 10 (5%) | 39 (20%) | 16 (8%) | 198 | 1.15 |
| Cat 5 | 82 (45%) | 18 (10%) | 9 (5%) | 48 (26%) | 25 (14%) | 182 | 1.54 |
| Totale | 302 (53%) | 71 (13%) | 30 (5%) | 114 (20%) | 51 (9%) | 568 | 1.19 |
| Si ricorda che il problema è stato affrontato nelle condizioni particolari del RMT: intera classe, allievi in completa autonomia, da 5 a 7 problemi da risolvere, un solo foglio risposta per problema. | |||||||
Criteri di attribuzione dei punteggi dell’analisi a priori del problema:
Da una accurata analisi è emerso che gli elaborati che hanno ottenuto il punteggio massimo hanno eseguito un ritaglio dei pezzi proposti, un abbinamento due a due degli stessi, facendoli combaciare. Tra questi, in diversi è stata messa in rilevanza la misurazione dei lati contando i lati della quadrettatura o usando il righello. Questa procedura ha permesso l’esclusione dei rettangoli singoli e non congruenti a due a due. L’individuazione delle facce ha permesso la costruzione o il disegno dell’unica scatolina possibile. La tecnica che ha dato maggiori risultati è risultata essere quella di utilizzare “lo sviluppo in piano” (30%), mentre solo il 15% ha usato il disegno tridimensionale e questi dati sono abbastanza comuni per tutte e tre le categorie. Il 15% consegna il foglio in bianco con un lieve decremento passando da categoria 3 a 5.
Molto frequente è stata la difficoltà a riconoscere i rettangoli congruenti. Non vi è stato il riconoscimento dell’utilità di considerare la misurazione corretta dei lati dei rettangoli ai fini di poter costruire o solo individuare la scatola.
Non sempre gli accoppiamenti hanno condotto alla capacità di ricostruire la scatola, compiendo errori di misurazione. Sono stati rilevati tentativi per riprodurre scatole con 5 facce oppure uso di 10 rettangoli per costruire lo sviluppo di una scatola. L’assenza di una visione tridimensionale dell’oggetto è stata molto frequente: è risultato difficile passare dal piano allo spazio, causa errori di assemblaggio e/o applicazione delle caratteristiche geometriche.
Sono stati anche registrati casi di applicazione di un ragionamento aritmetico completamente slegato dalla visione geometrica: 14:6= 2,2 con la convinzione di poter costruire due scatole con l’avanzo di due pezzi, ignorando completamente, ancora una volta, i vincoli delle caratteristiche geometriche da considerare.
Aver utilizzato le lettere minuscole per designare i cartoncini ha creato confusione tra le lettere b e q e tra p e d . In altri casi è stato usato più volte lo stesso cartoncino non rispettando le consegne ed in altri ancora è stato persino modificato il cartoncino del testo proposto, tagliandolo ulteriormente, per adeguarlo al tentativo di richiudere la scatola.
Il problema risulta poco adatto per gli alunni della scuola primaria, specialmente per la cat.3 e 4 (insuccessi tra il 70% e 80%).
Risulta evidente che questo problema richiede la capacità di saper vedere gli oggetti nella testa di un allievo di scuola primaria in tre dimensioni e saper passare dallo spazio al piano e viceversa. Inoltre è richiesta anche la capacità di misurare con una unità di misura già suggerita che non tutti riconoscono come tale, tant’è che diversi non riconoscono nemmeno la validità del “suggerimento “ e non lo sfruttano, anzi molti sono quelli che dichiarano che una volta ritagliati i pezzi fanno uso del righello per misurare i lati uguali.
Alla luce di questi risultati i può suggerire di iniziare fin da subito e poi intensificare il numero di esperienze attraverso le quali l’allievo si possa ritrovare a manipolare oggetti reali, come la scatola, per poi poterli riconoscere attraverso una rappresentazione iconica su un foglio e/o con le parti di cui sono composti (le facce). Tutto ciò risulta fondamentale quando ci si ritrova degli elaborati con la ricostruzione di scatole con cinque o sette facce! Oppure scatole copiate/disegnate molto bene sul foglio, ma completamente errata la ricostruzione reale della scatola stessa.
Alla fine è stato riconosciuto che il problema è difficile per una classe terza, mentre possibile per le classi quarte e quinte ai fini di un avvio allo studio del parallelepipedo.
Lo stesso problema è stato sperimentato su un campione di alunni frequentanti la classe prima della scuola secondaria di primo grado. I risultati ottenuti, anche se statisticamente poco significativi dato il numero esiguo di elaborati ( 18 gruppi di 3/5 alunni, quindi un campione di 70-80 alunni) ci possono comunque indicare una linea di tendenza; essi sono in linea con quelli ottenuti da cat.4 ( valore medio 1,07 ). Le condizioni della prova sono state queste: lavoro di gruppo di 3/5 alunni, tempo dato di soluzione, 25 minuti. Ecco i risultati:
Alla luce di questi risultati appare evidente che per cercare di migliorare questa situazione occorre lavorare fin dai primi anni della scuola primaria sulla geometria tridimensionale e, soprattutto, sulla manipolazione e costruzione di modelli. Queste attività inoltre devono essere portate avanti e sperimentate anche nella scuola secondaria di primo grado per creare una certa continuità di lavoro in modo da non generare negli alunni una conflittualità fra immagini mentali e concetti geometrici (vedi V. Villani, Geometria dello spazio, L’insegnamento della matematica e delle scienze integrate, vol.10,n°5). È indispensabile inoltre che il tempo di transizione dalla manipolazione di oggetti ai modelli e alla “matematizzazione” e astrazione avvenga nel modo più lento e adeguato possibile per agevolare l’assorbimento completo di tale fase.
G. Telatin, 2015, Ripartiamo da... 0 punti / Repartons du 0 point In. La Gazzetta di Transalpino / La Gazette de Transalpie, no 4, 2015, pp 95-114
(c) ARMT, 2009-2024