Le pré du père François (II)

Identification

Rallye: 18.II.19 ; catégories: 9, 10 ; domaines: FN, AL
Familles:

• MEQ - Etablir puis résoudre des (in)équations
• MEQ/EQ2 - Résoudre une équation du 2e degré
• RF - Traiter une relation fonctionnelle
• RF/TRI - Traiter une application quadratique

Remarque et suggestion

Résumé

Trouver les dimensions d’un rectangle d'aire 40 m² et de périmètre partiel (sur trois côtés) de 20 m, dans un contexte d’enclos rectangulaire protégé par un grillage (équation du second degré à racines irrationnelles à approcher convenablement).

Enoncé

Tâche de résolution et savoirs mobilisés

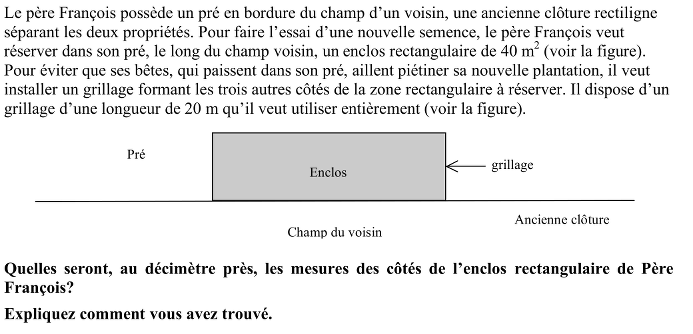
Il s’agit d'abord de s'approprier la situation et de comprendre que les côtés de la clôture peuvent varier, alors que l'aire du rectangle et la longueur de la clôture restent constants. Il faut ensuite traduire sous forme d’équations les relations entre les variables. Par exemple, si on appelle x la longueur du côté du rectangle parallèle à la vieille clôture (la base) et y celle du côté perpendiculaire (hauteur), on obtient les équations : xy = 40 et x + 2y = 20.

Plusieurs démarches sont alors possibles :

1) Travailler par essais, éventuellement en s'aidant d’un tableau. Les essais peuvent être effectués en fixant la valeur d'une variable ; on obtient alors la valeur de l'autre variable à partir d'une des deux équations et on utilise la seconde équation pour vérifier. Ou bien on peut faire varier en même temps les valeurs de x et y dans les deux formules.

2) Reconnaître l'ensemble des deux équations comme un système : les solutions à trouver pour x et y doivent être valables pour les deux les équations écrites. Pour le résoudre, il faut exprimer une variable en fonction de l'autre pour obtenir une équation à une inconnue ; par exemple remplacer dans la seconde équation y par 40/x, et obtenir l'équation du second degré : x² – 20x + 80 = 0.

On peut résoudre cette équation en utilisant la formule (seulement en cat.10) ou par approximations successives. Dans ce cas on peut considérer la fonction y = x² – 20x + 80 et donner à la variable x plusieurs valeurs de façon à trouver comme images pour y deux nombres de signes opposés. La recherche peut être faite d’abord avec des valeurs entières de x et on affine ensuite à partir des subdivisions en dixièmes des intervalles trouvés.

3) À partir des deux relations xy = 40 et x + 2y = 20, tracer les courbes correspondantes, déterminer les deux points d'intersection et interpréter leurs coordonnées dans le contexte du problème. Une autre résolution graphique possible consiste à tracer la parabole d’équation y = x² – 20x + 80 et à déterminer ses points d’intersection avec l’axe des abscisses. Une fois trouvées les deux solutions du problème, les donner avec l'approximation demandée.

Notions mathématiques

variables, fonctions, équations, graphique cartésien, approximation, aire, périmètre, nombres réels

Résultats

18.II.19

Le problème a été donné dans 142 classes de la catégorie 9 et 108 de la catégorie 10. Les résultats sont indiqués dans le tableau suivant:

Selon les critères déterminés lors de l’analyse a priori:

• 4 points: Les deux couples solutions (5,5 m et deux fois 7,3 m, ou 14,5 m et deux fois 2,8 m), avec une explication claire pour obtenir l’équation et une présentation de la démarche d’approximations ou la résolution par radicaux.
• 3 points: Les deux couples solutions, avec une explication claire pour obtenir l’équation, sans la méthode de résolution ou un résultat obtenu par tâtonnement non ordonné.
• 2 points: Un seul couple de solutions avec des explications cohérentes sur la manière de le trouver.
• 1 point: Démarche cohérente pour interpréter les données de l’énoncé et aboutir à une équation, sans sa résolution.
• 0 point: Incompréhension du problème ou non respect d’une contrainte.

Procédures, obstacles et erreurs relevés

Au préalable, signalons un obstacle dû à l'interprétation de la figure. Les élèves en déduisent à tort des informations supplémentaires, par exemple que la base doit être plus grande que la hauteur (avec comme conséquence une solution unique au problème) ou bien qu'il y a un rapport entre les côtés, à trouver par des mesures sur la figure.

Il est possible que l'insistance de l’énoncé à se référer à la figure (« voir la figure » répété deux fois) soit liée à cette interprétation. Une autre ambiguïté possible du texte est la forme de la question : « Expliquez comment vous avez trouvé votre réponse » qui peut faire penser à une solution unique.

Les procédures les plus utilisées sont la recherche par essais (cat.9) et la résolution de l'équation du second degré (cat.10) en utilisant la formule.

Dans le premier cas (procédure par essais) on remarque la difficulté à organiser les essais avec des nombres décimaux et à décrire les essais réalisés, qui souvent restent implicites. En outre la recherche s’arrête au premier essai satisfaisant, faisant perdre ainsi une des deux solutions du problème.

La seconde procédure (équation) met en évidence les difficultés de nature algébrique, liées à la résolution de l'équation du second degré. Dans les deux les cas, mais surtout dans la résolution algébrique où les solutions de l'équation sont écrites avec le symbole de la racine carrée, apparait le problème de la signification de l'approximation « au décimètre près» demandée.

Comme nous l’avons déjà dit, figure parmi les procédures erronées la lecture sur le schéma du rapport entre les côtés (exemple 1:3 ou bien 1:4), donnée qui est utilisée à la place d'une de celles de l’énoncé Dans plusieurs copies on observe l'hypothèse implicite (déduite de la figure) que la base doit être plus grande que la hauteur, restriction qui entraîne à ne pas considérer ou à exclure une des deux solutions du problème.

Exploitations didactiques

Dans le cadre du rallye, le problème a obtenu un pourcentage de succès très faible (surtout en cat.9). En effet ce problème, outre la capacité à mathématiser la situation par l'écriture d'un système et à déterminer les solutions de l'équation algébriquement ou graphiquement, demande d’autres capacités, comme celle de comprendre la situation sans se faire influencer par la figure proposée et celle de reconnaitre dans des nombres irrationnels les deux couples de solutions et éventuellement de les trouver par approximation. La richesse du problème constitue une ressource pour l'enseignant qui peut l'utiliser à différents moments de l’apprentissage et avec différents objectifs. En fonction de ces objectifs, l'enseignant peut même compléter ou partiellement modifier les questions du problème, entre autres pour lever les ambiguïtés du texte original signalées plus haut.

Proposons quelques exemples :

• Choix des variables et comparaison des équations obtenues. Le problème peut s'insérer dans l’apprentissage au début de l’algébrisation. Il constitue un exemple de situation dans laquelle l'écriture de l'équation à résoudre passe par l’écriture d'un système et dépend du choix des variables (on obtient des équations semblables mais différentes si x et y indiquent respectivement la base et la hauteur du rectangle ou vice-versa).
• Introduction des équations du second degré : le problème peut être utilisé pour faire naître l'exigence d'une méthode rapide et efficace pour la résolution de telles équations plutôt qu’une procédure de recherche par essais, longue et pas toujours fiable. À cet effet le problème peut être laissé sensiblement dans sa forme originale.
• Représentation de fonctions : le problème peut être utilisé pour donner des exemples de fonctions nées d'une situation géométrique et pour souligner le rapport de dépendance entre les variables. Dans ce but on pourrait ajouter la demande explicite d'une représentation (sous forme de tableau ou de graphique) de la fonction. En l’absence de cette demande, on observe en effet, que le recours à l’outil fonction (en particulier dans son registre graphique) n'est pas spontané. On peut associer au problème différents types de graphiques (hyperbole et droite, ou parabole, avec de légères variations aussi en relation avec le choix des variables). Un outil comme Geogebra peut être utilisé pour débarrasser les élèves des aspects techniques de la construction du graphique et focaliser leur attention sur l'interprétation même du graphique. Une comparaison entre les graphiques des figures 1 et 2 amène une réflexion sur les solutions du problème.

Le graphique de la figure 1 fournit les deux valeurs des inconnues x et y, alors que celui de la figure 2 fournit seulement les valeurs de x, celles de y devant être tirées de la relation utilisée, par substitution.

• Approximation : le problème peut être utilisé pour une réflexion sur la nature des nombres solutions. Il s'agit en effet de nombres irrationnels, qui peuvent être écrits en utilisant le symbole de la racine carrée, mais dont il est nécessaire de donner une valeur approchée dans une situation concrète (dans laquelle il est prévu par exemple l'achat de la clôture). Une variable didactique possible du problème peut être le degré d'approximation demandé. Il est à souligner que, en représentant les fonctions avec un logiciel comme Geogebra, la compréhension du concept de nombre irrationnel peut être favorisée grâce à l'exploration du graphique au moyen du « zoom » : le nombre irrationnel qui, initialement semble « à portée de main », devient, dans les agrandissements successifs, toujours plus inaccessible alors qu’augmente le nombre de chiffres de son écriture décimale. Dans la figure 3 on a représenté une des solutions du problème.

Pour aller plus loin

Voir la monographie.

Bibliographie

Henry, M. & Rizza, A. Six questions sur la notion de fonction dans les problèmes du RMT, Actes des journées d’études sur le Rallye mathématique transalpin, vol. 8, Brigue 2008. Eds. Lucia Grugnetti & François Jaquet, ARMT, 2009, p. 143-166.

Rizza, A. & Henry, M. Idea di funzione, Actes des journées d’études sur le Rallye mathématique transalpin, vol. 7, Bard (Valle d’Aosta) 2007. Eds. Lucia Grugnetti, François Jaquet, Gianna Bello, Rosanna Fassy, Graziella Telatin, ARMT, 2008, p. 181-198.

Henry, A., Henry M. & Rizza, A. Funzioni per risolvere problemi, La gazzetta di Transalpino, n.1, 2011, http://www.armtint.org/.

Groupe fonction (2010). Le pré du père François (II). Etude ARMT (http://www.projet-ermitage.org/ARMT/doc/etude-fn6-fr.pdf)

(c) ARMT, 2010-2024