
Banque de problèmes du RMT
fn8-fr
 |
Banque de problèmes du RMTfn8-fr |
|
Comparer le nombre de carrés unités contenus « sur le bord » d’un grand carré avec le nombre de petits carrés « intérieurs ». le nombre de petits carrés sur un bord varie de 3 à 20.
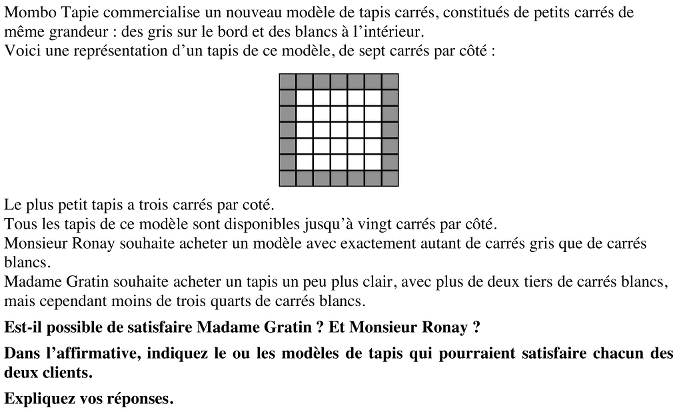
- Imaginer les tapis du modèle donné et en dessiner quelques-uns, parmi les plus simples.
- Comprendre les relations arithmétiques entre le nombre de carrés gris, le nombre de carrés blancs et le nombre de carrés sur un côté du tapis. Par exemple (en langage ordinaire) : le nombre de carrés gris est quatre fois le nombre de carrés sur le côté du tapis, moins les quatre carrés des angles qui seraient comptés deux fois ; et le nombre de carrés blancs est le nombre de carrés sur le côté du tapis, moins deux, puis élevé au carré.
- Noter les nombres de carrés de chaque couleur pour quelques tapis, puis se rendre compte qu’il faut en dresser un inventaire systématique (voir exemples suivant).
- Prendre en compte les demandes des clients et, par conséquent, calculer le rapport « carrés blanc / nombre total » pour voir les modèles qui conviennent.
Une analyse des rapports passe par la prise de conscience de leur croissance en fonction du nombre de carrés sur le côté : les tapis deviennent « de plus en plus clairs » car la partie blanche du centre croît plus rapidement que la bordure grise. On peut ainsi aboutir à un inventaire de ce genre, qui se limite aux modèles à envisager :
carrés par côté carrés gris carrés blancs carrés du tapis blancs/ total
3 8 (= 3 x 4 – 4) 1 = (3 – 2)^2 9 = 3^2 1/9 = 0,11…
... ... ... ... ...
6 20 (= 6 x 4) – 4) 16 = (6 – 2)^2 36 = 6^2 16/36 = 4/9 = 0,44…
7 24 25 49 25/49 = 0,51…
... ... ... ... ...
10 36 64 100 0,64 < 2/3
11 40 81 121 0,669…
12 44 100 144 0,694…
13 48 121 169 0,715…
14 52 144 196 0,734…
15 56 169 225 0.751… >3/4
16 60 196 256 0,765..
- Déduire de l’observation de la croissance des rapports « nombre de carrés blancs/nombre total de carrés » que la demande de M. Ronay ne pourra être satisfaite et que Mme Gratin pourra choisir entre les modèles de 11 à 14 carrés de côté.
carré, aire, périmètre, suite, dénombrement, rapport, équation, inéquation, calcul littéral, second degré
Sur 763 classes ayant participé à la première épreuve du 19e RMT, les points attribués à ce problème sont les suivants :
| Catégorie | 0 | 1 | 2 | 3 | 4 | Nb. de classes | Moyenne |
|---|---|---|---|---|---|---|---|
| Cat 8 | 239 (44%) | 121 (22%) | 113 (21%) | 42 (8%) | 23 (4%) | 538 | 1.05 |
| Cat 9 | 55 (43%) | 23 (18%) | 33 (26%) | 9 (7%) | 9 (7%) | 129 | 1.18 |
| Cat 10 | 38 (40%) | 17 (18%) | 23 (24%) | 9 (9%) | 9 (9%) | 96 | 1.31 |
| Total | 332 (44%) | 161 (21%) | 169 (22%) | 60 (8%) | 41 (5%) | 763 | 1.1 |
| Rappel: Le problème est résolu dans les conditions particulières du RMT: classe entière, élèves en autonomie complète, 5 à 7 problèmes à résoudre, une seule feuille de réponses par problème. | |||||||
On a relevé dans les copies les procédures suivantes, de la moins experte à la plus experte :
En majorité les productions des élèves montrent une démarche de type empirique, de types 1) ou 2) avec des essais plus ou moins organisés sur des listes et/ou des dessins et arrivent à une compréhension partielle du problème, la méthode empirique privilégiée étant de dessiner divers modèles de tapis. Pour les réponses plus élaborées, l'emploi d’un tableau met en évidence une démarche systématique permettant d'arriver au résultat correct.
Dans les catégories supérieures 9 et 10, on peut trouver quelques exemples de la procédure 4) mais, seulement dans de très rares cas, cette démarche algébrique est conduite de manière adéquate et aboutit à une réponse argumentée.
On observe dans la grande majorité des copies que la bonne réponse concernant M. Ronay est donnée sans justification, alors que pour répondre à la demande de Mme Gratin les élèves font ou tentent une vérification a posteriori. Un très petit nombre de copies utilisent implicitement le changement du signe de la différence « nombre de carrés gris moins nombres de carrés blancs » situé entre 6 et 7 petits carrés par côté, pour répondre que M. Ronay ne peut pas être satisfait. De même, très peu remarquent la croissance du rapport du nombre de petits carrés blancs sur le nombre total n2 de petits carrés.
Même sans tableau ou avec des tableaux ne contenant pas les colonnes représentant les exigences de Mme Gratin, 2n2/3 et 3n2/4, on trouve des copies calculant de tels rapports pour « vérifier » que Mme Gratin sera satisfaite avec des tapis de côté 11, 12, 13 ou 14 carrés.
Très peu d’élèves ont introduit la variable indépendante n du nombre de carrés par côté pour obtenir les fonctions qui lient les nombres des carrés gris et des carrés blancs au nombre n. D’ailleurs, dans les tableaux contenant les colonnes « nombre de carrés par côté », « nombre de carrés gris », « nombres de carrés blancs », « nombre total de carrés », souvent la colonne de ce qui est le plus logique de choisir comme « variable » (nombre de carrés par côté) n’est pas placée à la gauche du tableau.
Signalons que dans diverses productions les réponses 11 ou 14 pour le tapis de Mme Gratin ont été écartées, parfois un seul résultat (le 12) était donné.
Une dernière observation doit être faite concernant l’énoncé : la demande de Monsieur Ronay y précède celle de Madame Gratin, alors que l'ordre des questions est inversé. Ceci pourrait avoir désorienté certains élèves qui ont fait le choix d’une résolution de type algébrique et n’ayant pas abouti à un résultat pour M. Ronay, abandonnent.
Étant donné la très faible réussite à ce problème constatée sur 763 copies, il est raisonnable de conseiller de le proposer à des élèves en situation de classe, avec recherche individuelle, mises en commun de « pistes » et, suivant leur niveau, les inciter à construire des tableaux ou à mettre les données en équation.
La construction raisonnée d’un tableau aux niveaux 8 ou 9 peut mettre en évidence le rôle de la variable n du nombre de petits carrés par côté, comme donnée de base pour les calculs des nombres des carrés gris et blancs. Ce travail peut être considéré comme une première approche de la notion de fonction.
On peut adopter une résolution algébrique. Celle-ci conduit à une équation et deux inéquations du second degré, dont le traitement en nombres entiers peut se faire par essais et vérifications ou par une étude classique des trinômes obtenus.
Une réponse experte peut être de calculer en fonction du nombre n de petits carrés par côté le nombre total de carrés : n2, le nombre des carrés gris : 4n – 4 et celui des carrés blancs : (n – 2)2 . Pour la demande de Mme Gratin, on peut former le rapport du nombre de carrés blancs sur le nombre total : (n – 2)2/ n2 et le comparer à 2/3 et 3/4, ce qui conduit aux inéquations du deuxième degré : 8n2 < 12(n – 2)2 < 9n2 donnant les solutions entières 11, 12, 13, ou 14.
Pour la demande de M. Ronay, on peut résoudre l’équation : nombre de gris = nombre de blancs, (4n – 4) = (n – 2)2 qui n’a pas de solution entière. On obtient donc une impossibilité.
On peut aussi considérer que le rapport [n / (n – 2)]2 devrait être égal à 2, ce qui est impossible car sa racine carrée est irrationnelle.
Rinaldi, Maria Gabriella (1999). Bordures, Le Rallye Mathématique Transalpin. Quels profits pour la didactique? Actes des journées d’études sur le Rallye Mathématique Transalpin, Lucia Grugnetti & François Jaquet eds, Brigues 1997-1998, p. 67-70.
Groupe fonction (2014). Le retour de Mombo Tapie. Etude ARMT (http://www.projet-ermitage.org/ARMT/doc/etude-fn8-fr.pdf)
Inspiré par Bordure (04.F.12) et Tapis carrés (09.II.14)
(c) ARMT, 2011-2024